Tag Archives: policy

How Agent-based Models Offer Insights on Strategies to Mitigate Soil Degradation in North Korea: A Conversation with Dr. Yoosoon An

October 25, 2023 thesubmissionauthor Leave a comment

By Hyesop Shin¹ and Yoosoon An²

Interviewer: (HS), University of Glasgow, UK
Interviewee: (YA), Institute for Korean Regional Studies, Seoul National University, S.Korea.

Introduction

While there’s limited knowledge about North Korea’s farming system and food chain, it’s evident that soil degradation has been an ongoing concern for the nation. To gain deeper insights, I spoke with Dr. Yoosoon An, a renowned agent-based modeller from South Korea. His PhD research delved into land degradation and declining food production in North Korea during the 1990s using Agent-Based Modelling (ABM).

HS: Can you introduce yourself?

YA: Certainly. I’m Dr. Yoosoon An, a research fellow at the Institute for Korean Regional Studies at Seoul National University. My primary research interests are North Korea, Agent-Based Modelling, and the relationship between soil health and food security. I can’t believe I’ve been modelling ABM for nearly a decade!

HS: Can you give a brief overview of your research?

YA: During my academic journey, I was deeply intrigued by issues related to land degradation and landslides. But what really caught my attention was reading about the North Korean famine in the 1990s. It’s heartbreaking to think about it. Basically, in the mid-90s, North Korea faced this huge famine. It wasn’t just because of natural disasters like droughts, but also due to the economic chaos after the Soviet Union collapsed, and some big problems in their farming systems. This just destroyed their land, and so many people almost starved. You can find more details on its Wikipedia page.

HS: What part of social simulation would you like to introduce to the community?

YA: Well for ABM right? I’d like to introduce my PhD research that explored strategies to combat land degradation and food shortages in North Korea, with a special emphasis on the devastating famine of the 1990s (An 2020). Although there’s a clear connection between land degradation and famine, both issues are intricate and there’s limited information available, both in North Korea and globally. Through agent-based modelling (ABM), my study examined the interplay between land degradation and the decline in food production as a pivotal factor behind North Korea’s major famine in the 1990s. This “vicious cycle of land degradation”, where agricultural productivity drops because of worsening land conditions, and then the land degrades further as people intensively cultivate it to compensate, plays a central role in the broader challenges of devastation, famine, and poverty.

I utilised ABM to look at land cover changes and posited scenarios to hypothesise the potential outcomes, given alternate policies during the 1990s. Through this research, I aimed to unravel the intricacies of the relationship between land degradation and food production, providing insights that may pave the way for future policy development and intervention strategies in analogous situations.

HS: So, you’re focusing on the famine from the ’90s, but what made you decide to simulate from the 1960s?

YA: The 1960s hold significance for several key reasons. After North Korea adopted the “shared ownership system” in 1946, private land ownership was permitted. But by 1960, following the Korean War, these private lands had been integrated into collective farms. Most of today’s agricultural practices in North Korea can be traced back to that period. Furthermore, my research pointed out a noticeable increase in documentation and data collection beginning in the 1960s, underscoring its importance. From a socio-ecological perspective, I believe that the famine was a culmination of multiple intersecting crises including the one that took place in 1995. Starting the simulation from the 1960s, and tracking land cover changes up to 2020, seemed the most comprehensive approach to understanding the intricate dynamics at play.

The Agent-based Model: the “North Korean Collective Farm”

HS: Let’s delve deeper into your model. The incorporation of both land use and human agents is particularly fascinating. Could you break down this concept figure for us before we discuss the simulation?

YA: Of course. If you refer to Figure 1, it visually represents the farm’s layout and topography. We’ve chosen to represent it through simplified square and ski-slope shapes. The model also integrates the initial forest cover to demonstrate the degradation that occurred when forests were converted into farmland. When setting the model, we positioned different land uses based on the environmental adaptation strategies traditional to the Korean people. So, you’ll notice the steeper forests situated to the north, the flatter rice fields to the south, and the villages strategically placed along the mountain edge.

YA: To give you a broader picture, the model we’ve termed the “North Korean Collective Farm” (as shown in Figure 1) is a composite representation of collective farms. In this model, a collective farm is visualised as a community where several farmers either co-own their land, reflecting cooperative farming practices (akin to the “Kolkhoze” in the Soviet Union) or as part of a state-owned agricultural entity (resembling the state farm or “Sovkhozy” from the Soviet Union). North Korea embraced this model in 1954 and by 1960 had fully transitioned all its farms into this system. While there’s a dearth of comprehensive data about North Korean collective farms, a few studies offer some general insights. Typically, a farm spans between 550 and 750 hectares, roughly equivalent to ‘Ri’, North Korea’s smallest administrative unit. On average, each of these farms accommodates 300-400 households, which translates to 700-900 active workers and a total of 1900-2000 residents. These farms are further segmented into 5-10 workgroups, serving as the foundational unit for both farming activities and the distribution of yield.

HS: So, in areas where there’s a lack of specific data or where details are too diverse to be standardised, you’ve employed abstraction and summarisation. This approach to modelling seems pragmatic. When you mention setting the initial agricultural land cover to 30% rice fields and 70% other farmland, is this a reflection of the general agricultural makeup in North Korea? Would this distribution be typical or is it an average derived from various sources?

YA: Exactly. Given the limited and sometimes ambiguous data regarding North Korea, abstraction and summarization become invaluable tools for our model. The 30% rice fields and 70% other farmland distribution is a generalised representation derived from an aggregate of available North Korean land use data. While it might not precisely mirror any specific farm, it provides a reasonable approximation of the agricultural landscape across the region. This method allows us to capture the essential features and dynamics without getting mired in the specifics of any one location.

Fig 1

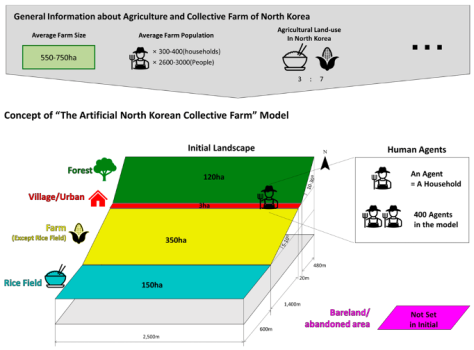
Figure 1. Conceptual model of the Artificial North Korean Collective Farm: integrating land use and human agents to build an agent-based model for mitigating famine risk in North Korea.

HS: Okay so let’s talk about agents. So, you’ve focused on the ‘cooperative farm’ as a representative agent in your model. This is essentially to capture the intricacies of the North Korean agricultural landscape. Can you expand a bit more on how the ‘cooperative farm’ reflects the realities of North Korean agriculture and how the LUDAS framework enhances this?

YA: Certainly. The ‘cooperative farm’ or ‘cooperative household’ is more than just a symbolic entity. It encapsulates the very essence of North Korean agricultural practices. Beginning in the 1960s and persisting to the present day, these cooperative structures are foundational to the nation’s farming landscape. Notably, their geographical boundaries often align with administrative units, making them not just agricultural but also socio-political entities. When we employ broader system dynamics models that span the entirety of North Korea, often the granularity and the subtleties can get lost. Hence, zooming into the cooperative farm level provides us with the precision and detail needed to observe intricate dynamics and interactions.

YA: Another important reason is to apply the Land-use dynamic simulator (LUDAS) framework for the case of North Korea. Now, speaking of LUDAS – this framework was chosen for its ability to seamlessly bridge biophysical and socio-economic parameters. It’s a holistic approach that factors in long-term land use/cover changes against a backdrop of varied management, planning, and policy scenarios. The strength of LUDAS lies in its capability to encapsulate the intertwined dynamics of human-environment interactions. Through a multi-agent simulation process, LUDAS effectively mirrors real-world causal mechanisms, feedback loops, and interactions. By integrating this framework into our model, we aimed to offer a comprehensive portrayal of North Korea’s agricultural landscape, rich in both depth and breadth.

HS: How do the agents decide their actions and movements?

YA: Agent decisions are based on a simple principle: when they require more food, they change their work strategy and land use. Their decisions are divided into two categories: labour allocation and land-use changes. If their labour-to-food demand ratio exceeds 1, they redirect their labour and change their land use. If this ratio is less than one, they will stick to their previous strategies.

YA: In terms of labour allocation, we assume that a worker is available 300 days per year, working 8 hours per day. The minimum labour required to cultivate an average crop on a 100m² rice field is 36 hours per year and 48 hours for other crops. These figures are based on South Korean farming data because North Korean data is unavailable. Our model initially used 6 hours for rice and 8 hours for other crops, but these settings had no effect. As a result, we changed the hours to better reflect conditions in North Korea.

YA: Agents with a food demand ratio of less than one will allocate their labour time based on our initial assumption (if this is the first year) or on the previous year’s allocation. If the ratio exceeds one, they adjust their time allocation based on soil productivity. They will first reduce or eliminate investment in less productive lands, then devote more time to more fertile areas. The labour efficiency metric is determined by comparing the current labour time to the initially assumed time. If you have time you can take a look at Equation (3) mentioned in the paper (An & Park 2023).

HS: So, in essence, how does this environment shape the behaviour and choices of the agents?

YA: The agents operate within the landscape-environmental system, which is a subsystem influenced by the LUDAS framework. This system offers a detailed insight into land degradation and food production processes specific to North Korea. Comprising five unique submodules, it considers the biological, physical, and chemical properties of the soil, coupled with a quality index for the soil and a final metric that evaluates potential food yield by integrating these factors. All these elements together determine how agents adapt and make decisions based on the changing environment.

HS: How did you decide on a one-year interval for your simulation, especially in the context of Discrete Event Simulation?

YA: In places with a temperate to cold climate like North Korea, farming activities primarily follow an annual rhythm. Apart from this agricultural reasoning, my decision was, in part, based on the data availability. The datasets I had access to didn’t provide more detailed time frames. However, considering that many nations’ agricultural practices revolve around an annual cycle, it made sense to align both environmental and socioeconomic indicators with this timeframe. Still, I’m eager to eventually incorporate more granular data, such as monthly datasets, to explore the nuanced seasonal changes in land cover.

HS: Can you explain this loop diagram for us?

YA: The diagram presents a feedback loop related to land use happening every year in the simulation. When land productivity goes down because of overuse, there’s a greater demand for food. This greater demand then causes people to use the land more, further decreasing its quality. This continuous cycle results in ongoing harm to the land, and thus increases the food pressure for the agents also known as cooperative farms.

YA: Essentially, the loop demonstrates that “lower land productivity leads to more demand for food, which then causes even more intensive land use, further reducing the land’s quality.” In our study, we noticed that as the quality of the land decreased steadily, the decrease in the food it produced was much faster. This suggests that the effects get stronger with each cycle due to the feedback loop.

Fig 2

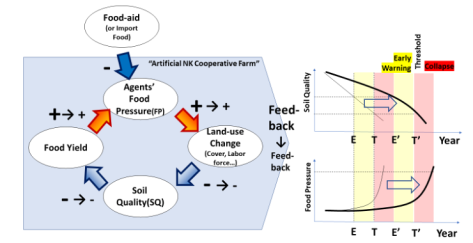
Figure 2. A feedback loop that connects land degradation and soil quality, subsequently inducing food pressure on agents. Within this loop, two critical points are identified: “E,” representing an early warning signal, and “T,” representing a threshold. Crossing this threshold can lead to a systematic collapse.

HS: Given the challenges associated with gathering information on North Korea, how did you ensure the validity of your model’s results?

YA: Validating the outcomes, especially for North Korea, was indeed challenging. For the environmental aspects, we relied on satellite imagery and referenced previous research data to validate our variables. When it came to the human agents, we tapped into an extensive array of literature and data on North Korean cooperative farms. We kept the behavioural rules for these agents straightforward, for instance, they’d modify their behaviours when faced with hunger, prioritise maximising land productivity, and turn to inter-mountain cultivation if they encountered continued food shortages. As for variables like labour hours and land potential, we began with South Korean data due to the absence of precise data from the North. Then, based on the outcomes of our iterative simulations, we made necessary adjustments to ensure the model aligned as closely as possible with reality.

HS: Before we dive into the findings, I just wanted to hear your opinion on Proof-Of-Concept (POC) models because you employed POC for your simulation. Can you discuss the advantages and limitations of using such models?

YA: POC models are particularly effective in scenarios with limited data availability. Despite the data constraints from North Korea, the consistency in their reports allowed me to simulate the progression of land degradation over time. POC models often have an intuitive interface, enabling easy adjustments and scenario applications. Debugging is also straightforward. However, the results can sometimes lack precise real-world applicability. Adding data or algorithms necessitates an abstraction process, which can introduce inaccuracies. For instance, equating one grid pixel to a household can oversimplify the model. Additionally, the interface might sometimes be less intuitive.

YA: I aimed to represent the food sustainability and socio-ecological systems in northeastern Asia, encompassing both China and the Korean peninsula. However, due to the lack of data for North Korea, I used a Proof-of-Concept model instead.

Findings

HS: From your simulations, what were the main insights or conclusions you drew?

YA: Our baseline simulation of the North Korean cooperative farm model painted a concerning picture. It revealed a vicious cycle where land degradation led to decreased food production, eventually culminating in a famine. Beginning the simulation from 1960, our model anticipated a famine occurring approximately 35 years later, which aligns with the real-world famine of 1995 in North Korea. You can take a look at Figure 3.

YA: On introducing the additional food supply scenario, we observed a delay in the onset of the famine. This finding highlights the significance of addressing the isolated nature of North Korea when aiming to prevent famine. However, it’s imperative to understand that merely making the food system more accessible isn’t a silver bullet. Comprehensive solutions must also focus on various other interventions.

HS: Based on your research, what are the potential solutions to address the future food crisis in North Korea?

YA: Our model highlights a feedback loop that intensifies food scarcity as land quality degrades. One approach we tested was enhancing external food supply. The results showed that this strategy can slow down the threat of famine, but it doesn’t completely break the loop. Even with more food coming in, the core issue—deteriorating land quality—remains unresolved.

YA: Several alternatives to address this feedback loop include adopting sustainable agricultural practices, supplementing with external energy sources, or restructuring North Korea’s collective farming system. We’re still working on modelling these solutions effectively.

YA: Historically, the Korean Peninsula faced severe famines in the 1600s, attributed to factors like climatic changes, deforestation, and diplomatic isolation. These circumstances resemble North Korea’s recent famine in the 1990s. The underlying problem in both cases is a cycle where declining land productivity demands more food production, further harming the land.

YA: Considering this historical context, it’s possible to argue that the Korean Peninsula, by itself, might not sustain its population and environment without external help. Supplying food and energy from outside might be more of a temporary solution, giving us time to seek more permanent ones.

YA: To genuinely address the land and food problem, we need to explore and test alternatives further. This could involve sustainable farming methods, efficient agricultural systems, and broader diplomatic actions for international trade and cooperation. The ultimate goal is a sustainable future for both North Korea and the entire Korean Peninsula.

Fig 3

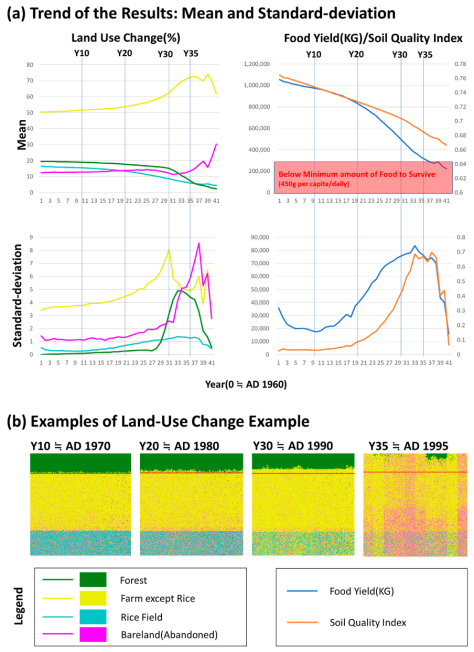
Figure 3. Summary of the results for replicability of the great famine in the 1990s: (a) Mean and standard deviation trends of land-use change (left) and food yield and soil quality (right); (b) Examples of land-use change in the model (NetLogo Interface)

Policy modelling requires a multi-scale, multi-criteria and diverse-framing approach

July 31, 2023 thesubmissionauthor 2 Comments

Lessons from a session at SocSimFest 2023

By Gary Polhill and Juliette Rouchier

Bruce Edmonds organized a stimulating session at the SocSimFest held 15-16 March 2023. Entitled, “How to do wrong using Social Simulation – as a result of arrogance, laziness or ill intent.” One of the presentations (Rouchier 2023) covered the modelling used to justify lockdowns in various countries. This talk concentrated on the harms lockdowns caused and suggested that they were unnecessary; a discourse that is not the most present in the media and takes an alternative view to the idea that a scientific consensus exists in real-time and could lead to the best decision. There was some ‘vigorous’ debate afterwards, but here we expand on an important point that came out of that debate: Modelling the effects of Covid to inform policy on managing the disease requires much more than epidemiological modelling. We might speculate, then, whether in general, modelling for policy intervention means ensuring greater coverage of the wider system than might be deemed strictly necessary for the immediate policy question in hand. Though such speculation has apparent consequences for model complicatedness that go beyond Sun et al.’s (2016) ‘Medawar zone’ for empirical ABM, there is an interpretation of this requirement for extended coverage that is also compatible with preferences for simpler models.

Going beyond the immediate case of Covid would require the identification of commonalities in the processes of decision making that could be extrapolated to other situations. We are less interested in that here than making the case that simulation for policy analysis in the context of Covid entails greater coverage of the system than might be expected given the immediate questions in hand. The expertise of Rouchier means our focus is primarily on the experience of Covid in France. Generalisation of the principle to wider coverage beyond this case is a matter of conjecture that we propose making.

Handling Covid: an evaluation that is still in progress

Whether governments were right or wrong to implement lockdowns of varying severity is a matter that will be for historians to debate. During that time various researchers developed models, including agent-based models, that were used to advise policymakers on handling an emergency situation predicated on higher rates of mortality and hospitalisation.^[1] Assessing the effectiveness of the lockdowns empirically would require us to be able to collect data from parallel universes in which they were not implemented. The fact that we cannot do this leaves us, as Rouchier pointed out, either comparing outcomes with models’ predictions – which is problematic if the models are not trusted – or comparing outcomes across countries with different lockdown policies – which has so far been inconclusive even if it weren’t problematic because of differences in culture and geography from one nation to another. Such comparison will nevertheless be the most fruitful in time, although the differences of implementation among countries will doubtless induce long discussions about the most important factors to consider for defining relevant Non-Pharmaceutical Interventions (NPI).^[2]

The effects of the lockdowns themselves on people’s mental and physical health, child development, and on the economy and working practices, are also the subject of emerging data post-lockdown. Some of these consequences have been severe – not least for the individuals concerned. Though not germane to the central argument of this brief document, it is worth noting that the same issue with unobservable parallel universes means that scientific rather than historical assessment of whether these outcomes are better or worse than any outcomes for those individuals and society at large in the absence of lockdowns is also impossible.

For our purposes, the most significant aspect of this second point is that the discussion has arisen after the epidemic emergency: First, it is noteworthy that these matters could perfectly well have been considered in models during the crisis. Indeed, contrasting the positive effect (saving lives or saving a public service) with negative effects (children’s withdrawal from education,^[3] increasing psychological distress, not to mention domestic abuse – Usta et al. 2021) is typically what cost-benefit analysis, based on multi-criteria modelling, is supposed to elicit (Roy, 1996). In modelling for public policy decision-making, it is particularly clear that there is no universally ‘superior’ or ‘optimum’ indicator to be used for comparing options; but several indicators to evaluate diverse alternative policies. A discussion about the best decision for a population has to be based on the best description of possible policies and their evaluations according to the chosen indicators (Pluchinotta et al., 2022). This means that a hierarchy of values has to be made explicit to justify the hierarchy of most important indicators. During the Covid crisis one question that could have been asked (should it not have been) is: who is the most vulnerable population to protect? Is it old people because of disease or young people because of potential threats to their future chances in life?

Second, it is clear that this answer could vary in time with information and the dynamics of variant of Covid. For example, as soon as Omicron was announced by South Africa’s doctors, it was said to be less dangerous than earlier variants.^[4] In that sense, the discussion of balancing priorities, in a dynamic way, in this historical period is very typical of what could also be central in other public discussions where the whole population is facing a highly uncertain future, and where the evolution of knowledge is rapid. But it is difficult to know in advance which indicators should be considered since some signals can be very weak at some point in time, but then be confirmed as highly relevant later on – essentially this is the problem of the omitted-variable bias.

The discussion about risks to mental health was vivid in 2020 already: some psychologists were soon showing the risk for people with mental health issues or women with violent husbands;^[5] while the discussion about effects on children started early in 2020 (Singh et al., 2020). However this issue only started to be considered publicly by the French government a year and a half later. One interpretation of the time differential is that the signal seemed too weak for non-specialists early on, when the specialists had already seen the disturbing signs.

In science, we have no definitive rule to decide when a weak signal at present will later turn out to be truly significant. Rather, it is ‘society’ as a whole that decides on the value of different indicators (sometimes only with the wisdom of hindsight) and scientists should provide knowledge on these. This goes back to classical questions of hierarchy of values about the diverse stakes people hold in questions that recur perennially in decision science.

Modelling for policy making: tension between complexity and elegance?

Edmonds (2022) presented a paper at SSC 2022 outlining four ‘levels’ of rigour needed when conducting social simulation exercises, reserving the highest level for using agent-based models to inform public policy. Page limitations for conference submissions meant he was unable to articulate in the paper as full a list of the stipulations for rigour in the fourth level as he was for the other three. However, Rouchier’s talk at the SocSimFest brought into sharp focus that at least one of those stipulations is that models of public policy should always have broader coverage of the system than is strictly necessary for the immediate question in hand. This has the strange-seeming consequence that exclusively epidemiological models are inadequate to the task of modelling how a contagious illness should be controlled. For any control measure that is proposed, such a stipulation entails that the model be capable of exploring not only the effect on disease spread, but also potential wider effects of relevance to societal matters generally in the domain of other government departments: such as, energy, the environment, business, justice, transportation, welfare, agriculture, immigration, and international relations.

The conjecture that for any modelling challenge in complex or wicked systems, thorough policy analysis entails broader system coverage than the immediate problem in hand (KIDS-like – see Edmonds & Moss 2005), is controversial for those who like simple, elegant, uncomplicated models (KISS-like). Worse than that, while Sun et al. (2016), for example, acknowledge that the Medawar zone for empirical models is at a higher level of complicatedness than for theoretical models, the coverage implied by this conjecture is broader still. The level of complicatedness implied will also be controversial for those who don’t mind complex, complicated models with large numbers of parameters. It suggests that we might need to model ‘everything’, or that policy models are then too complicated for us to understand, and as a consequence, perhaps using simulations to analyse policy scenarios is inappropriate. The following considers each of these objections in turn with a view to developing a more nuanced analysis of the implications of such a conjecture.

Modelling ‘everything’ is a matter that is the easiest to reject as a necessary implication of modelling ‘more things’. Modelling, say, the international relations implications of proposed national policy on managing a global pandemic, does not mean one is modelling the lifecycle of extremophile bacteria, or ocean-atmosphere interactions arising from climate change, or the influence of in-home displays on domestic energy consumption, to choose a few random examples of a myriad things that are not modelled. It is not even clear what modelling ‘everything’ really means – phenomena in social and environmental systems can be modelled at diverse levels of detail, at scales from molecular to global. Fundamentally, it is not even clear that we have anything like a perception of ‘everything’, and hence no basis for representing ‘everything’ in a model. Further, the Borges argument^[6] holds in that having a model that would be the same as reality makes it useless to study as it is then wiser to study reality directly. Neither universal agreement nor objective criteria^[7] exist for the ‘correct’ level of complexity and complication at which to model phenomena, but failing to engage with a broader perspective on the systemic effects of phenomena leaves one open to the kind of excoriating criticism exemplified by Keen’s (2021) attack on economists’ analysis of climate change.

At the other end of the scale, doing no modelling at all is also a mistake. As Polhill and Edmonds (2023) argue, leaving simulation models out of policy analysis essentially makes the implicit assumption that human cognition is adequate to the task of deciding on appropriate courses of action facing a complex situation. There is no reason (besides hubris) to believe that this is necessarily the case, and plenty of evidence that it is not. Not least of such evidence is that many of the difficult decisions we now face around such things as managing climate change and biodiversity have been forced upon us by poor decision-making in the past.

Cognitive constraints and multiple modellers

This necessity to consider many dimensions of social life within models that are ‘close enough’ to the reality to convince decision-makers induces a risk of ‘over’-complexity. Its main default is the building of models that are too complicated for us to understand. This is a valid concern in the sense that building an artificial system that, though simpler than the real world, is still beyond human comprehension, hardly seems a worthwhile activity. The other concern is that of the knowledge needed by the modeller: how can one person be able to imagine an integrative model which includes (for example) employment, transportation, food, schools, international economy, and any other issue which is needed for a serious analysis of the consequences of policy decisions?

Options that still entail broader coverage but not a single overcomplicated integrated model are: 1/ step-by-step increase in the complexity of the model in a community of practitioners; 2/ confrontation of different simple models with different hypotheses and questions; 3/ superposition and integration of simple models into one, through a serious work on the convergence of ontologies (with a nod to Voinov and Shugart’s (2013) warnings).

To illustrate this first approach, let us stay with the case of the epidemic model. One can start with an epidemiological simulation where we fit to the fact that if we tell people to stay at home then we will cut hospitalizations by enough that health services will not be overwhelmed. But then we are worried that this might have a negative impact on the economy. So we bring in modelling components that simulate all four combinations of person/business-to-person/business transactions, and this shows that if we pay businesses to keep employees on their books, we have a chance of rebooting the economy after the pandemic is over.^[8] But then we are concerned that businesses might lie about who their employees are, that office-workers who can continue to work at home are privileged over those with other kinds of job, that those with a child-caring role in their households are disadvantaged in their ability to work at home if the schools are closed, and that the mental health of those who live alone is disproportionately impacted through cutting off their only means of social intercourse. And so more modelling components are brought in. In a social context, this incremental addition of the components of a complicated model may mean it is more comprehensible to the team of modellers.

If the policy maker really wants to increase her capacity to understand her possible actions with models, she would also have to make sure to invite several researchers for each modelled aspect, as no single social science is free of controversy, and the discussions about consequences should rely on contradictory theories. If a complex model has to be built, it can indeed propose different hypotheses on behaviours, functioning of economy, sanitary risks depending on the type of encounter.^[9] It is then more of a modelling ‘framework’ with several options for running various different specific models with different implementation options. One advantage of modelling that applies even in cases where Borges argument applies, is that testing out different hypotheses is harmless for humans (unlike empirical experiments) and can produce possible futures, seen as trajectories that can then be evaluated in real time with relevant indicators. With a serious group of modellers and statisticians, providing contradicting views, not only can the model be useful for developing prospective views, but also the evaluation of hypotheses could be done rapidly.
The CoVprehension Collective (2020) showed another approach, more fluid in its organisation. The idea is “one question, one model”, and the constraint is to have a pedagogic result where a simple phenomenon would be illustrated. Different modellers could realise one or several models on simple issues, so that to explain one simple phenomenon, paradox or show a tautological affirmation. In the process, the CoVprehension team would create moving sub-teams, associate on one specific issue and propose their hypotheses and results in a very simple manner. Such a protocol was purely oriented for explanation to the public, but the idea would be to organise a similar dynamic for policy makers. The system is cheap (it was self-organised with researchers and engineers, with zero funding but their salary) and it sustained lively discussions, with different points of view. Questions could go from differences between possible NPI, with an algorithmic description of these NPI that could make the understanding of processes more precise, to an explanation of the reason why French supermarkets were missing toilet paper. Twenty questions were answered in two months, thus indicating that such a working dynamic is feasible in real-time and provides useful and interesting inputs to discussion.
To avoid too complicated a model, the fusion of both approaches could also be conceived: the addition of dimensions to a large central model could be first tested through simple models, the main process of explanation could be found and this process reproduced within the theoretical framework of the large model. This would constitute both a production of diversity of points of view and models and the aggregation of all points of view in one large model. The fact that the model should be large is important, as ‘size matters’ in diffusion models (e.g. Gotts & Polhill 2010), and thus simple, small models would benefit from this work as well.

As some modellers like complex models (and can think with the help of these models) and others rely on simple stories to increase their understanding of the world, only the creation of an open community of diverse specialists and modellers, KISS as well as KIDS, such a collective step-by-step elaboration could resolve the central problem that ‘too complicated to understand’ is a relative, rather than absolute, assessment. One very important prerequisite of such collaboration is that there is genuine ‘horizontality’ of the community: where each participant is listened to seriously whatever their background, which can be an issue in interdisciplinary work, especially involving people of mixed career stage. Be that as it may, the central conjecture remains: agent-based modelling for policy analysis should be expected to involve even more complicated (assemblages of) models than empirical agent-based modelling.

Endnotes

^[1] This point is the one that is the most disputed ex-post in France, where lockdowns were justified (as in other countries) to “protect hospitals”. In France, the idea was not to avoid deaths of older people (90% of deaths were people older than 60, this demographic being 20% of the population), but to avoid hospitals being overwhelmed with Covid cases taking the place of others. In France, the official data regarding hospital activity states that Covid cases represented 2% of hospitalizations and 5% of Intensive Care Unit (ICU) utilizations. Further, hospitals halved their workload from March to May 2020 because of almost all surgery being blocked to keep ICUs free. (In October-December 2020, although the epidemic was more significant at that time, the same decision was not taken). Arguably, 2% of 50% not an increase that should destroy a functioning system – https://www.atih.sante.fr/sites/default/files/public/content/4144/aah_2020_analyse_covid.pdf – page 2. Fixing dysfunction in the UK’s National Health Services has been a long-standing, and somewhat tedious, political and academic debate in the country for years, even before Covid (e.g. Smith 2007; Mannion & Braithwaite 2012; Pope & Burnes 2013; Edwards & Palmer 2019).

^[2] An interesting difference that French people heard about was that in the UK, people could wander on the beaches during lockdowns, whereas in France it was forbidden to go to any natural area – indeed, it was forbidden to go further than one kilometre from home. Whereas, in fact, in the UK the lockdown restrictions were a ‘devolved matter’, with slightly different policies in each of the UK’s four member nations, though very similar legislation. In England, Section 6 paragraph (1) of The Health Protection (Coronavirus, Restrictions) (England) Regulations 2020 stated that “no person may leave the place where they are living without reasonable excuse”, with paragraph (2) covering examples of “reasonable excuses” including for exercise, obtaining basic necessities, and accessing public services. Similar wording was used by other devolved nations. None of the regulations stipulated any maximum distance from a person’s residence that these activities had to take place – interpretation of the UK’s law is based on the behaviour of the ‘reasonable person’ (the so-called ‘man on the Clapham omnibus’ – see Łazowski 2021). However, differing interpretations of what ‘resonable people’ would do between the citizenry and the constabulary led to fixed penalty notices being issued for taking exercise more than five miles (eight kilometres) from home – e.g. https://www.theguardian.com/uk-news/2021/jan/09/covid-derbyshire-police-to-review-lockdown-fines-after-walkers-given-200-penalties In Scotland, though the Statutory Instrument makes no mention of any distance, people were ‘given guidance’ not to travel more than five miles from home for leisure and recreation, and were still advised to stay “within their local area” after this restriction was lifted (see https://www.gov.scot/news/travel-restrictions-lifted/).

^[3] A problem which seems to be true in various countries https://www.unesco.org/en/articles/new-academic-year-begins-unesco-warns-only-one-third-students-will-return-school
https://www.kff.org/other/report/kff-cnn-mental-health-in-america-survey/
https://eu.usatoday.com/in-depth/news/health/2023/05/15/school-avoidance-becomes-crisis-after-covid/11127563002/#:~:text=School%20avoidant%20behavior%2C%20also%20called,since%20the%20COVID%2D19%20pandemic
https://www.bbc.com/news/health-65954131

^[4] https://www.cityam.com/omicron-mild-compared-to-delta-south-african-doctors-say/

^[5] https://www.terrafemina.com/article/coronavirus-un-psy-alerte-sur-les-risques-du-confinement-pour-la-sante-mentale_a353002/1

^[6] In 1946, in El hacedor, Borges described a country where the art of building maps is so excessive in the need for details that the whole country is covered by the ideal map. This leads to obvious troubles and the disappearance of geographic science in this country.

^[7] See Brewer et al. (2016) if the Akaike Information Criterion is leaping to your mind at this assertion.

^[8] Although this assumption might not be stated that way anymore, as the hypothesis that many parts of the economy would hugely suffer started to reveal its truth even before the end of the crisis: a problem that had only been anticipated by a few prominent economists (e.g. Boyer, 2020). This failure shows mainly that the description that most economists make of the economy is too simplistic – as often reproached – to be able to anticipate massive disruptions. Everywhere in the world the informal sector was almost completely stopped as people could neither work in their job nor meet for information market exchange, which causes misery for a huge part of the earth population, among the most vulnerable (ILO, 2022).

^[9] A real issue that became obvious is that the nosocomial infections are (still) extremely important in hospitals, as the evaluation of the number of infections in hospitals for Covid19 are estimated to be 20 to 40% during the first epidemic (Abbas et al. 2021).

Acknowledgements

GP’s work is supported by the Scottish Government Rural and Environment Science and Analytical Services Division (project reference JHI-C5-1).

References

Abbas, M., Nunes, T. R., Martischang, R., Zingg, W., Iten, A., Pittet, D. & Harbarth, S. (2021) Nosocomial transmission and outbreaks of coronavirus disease 2019: the need to protect both patients and healthcare workers. Antimicrobial Resistance & Infection Control 10, 7. doi:10.1186/s13756-020-00875-7

Boyer, R. (2020) Les capitalismes à l’épreuve de la pandémie, La découverte, Paris.

Brewer, M., Butler, A. & Cooksley, S. L. (2016) The relative performance of AIC, AIC_C and BIC in the presence of unobserved heterogeneity. Methods in Ecology and Evolution 7 (6), 679-692. doi:10.1111/2041-210X.12541

the CoVprehension Collective (2020) Understanding the current COVID-19 epidemic: one question, one model. Review of Artificial Societies and Social Simulation, 30th April 2020. https://rofasss.org/2020/04/30/covprehension/

Edmonds, B. (2022) Rigour for agent-based modellers. Presentation to the Social Simulation Conference 2022, Milan, Italy. https://cfpm.org/rigour/

Edmonds, B. & Moss, S. (2005) From KISS to KIDS – an ‘anti-simplistic’ modelling approach. Lecture Notes in Artificial Intelligence 3415, pp. 130-144. doi:10.1007/978-3-540-32243-6_11

Edwards, N. & Palmer, B. (2019) A preliminary workforce plan for the NHS. British Medical Journal 365 (8203), I4144. doi:10.1136/bmj.l4144

Gotts, N. M. & Polhill, J. G. (2010) Size matters: large-scale replications of experiments with FEARLUS. Advances in Complex Systems 13 (04), 453-467. doi:10.1142/S0219525910002670

ILO Brief (2020) Impact of lockdown measures on the informal economy, https://www.ilo.org/global/topics/employment-promotion/informal-economy/publications/WCMS_743523/lang–en/index.htm

Keen, S. (2021) The appallingly bad neoclassical economics of climate change. Globalizations 18 (7), 1149-1177. doi:10.1080/14747731.2020.1807856

Łazowski, A. (2021) Legal adventures of the man on the Clapham omnibus. In Urbanik, J. & Bodnar, A. (eds.) Περιμένοντας τους Bαρβάρους. Law in a Time of Constitutional Crisis: Studies Offered to Mirosław Wyrzykowski. C. H. Beck, Munich, Germany, pp. 415-426. doi:10.5771/9783748931232-415

Mannion, R. & Braithwaite, J. (2012) Unintended consequences of performance measurement in healthcare: 20 salutary lessons from the English National Health Service. Internal Medicine Journal 42 (5), 569-574. doi:10.1111/j.1445-5994.2012.02766.x

Pluchinotta I., Daniell K.A., Tsoukiàs A. (2002), “Supporting Decision Making within the Policy Cycle: Techniques and Tools”, In M. Howlett (ed.), Handbook of Policy Tools, Routledge, London, 235 – 244. https://doi.org/10.4324/9781003163954-24.

Polhill, J. G. & Edmonds, B. (2023) Cognition and hypocognition: Discursive and simulation-supported decision-making within complex systems. Futures 148, 103121. doi:10.1016/j.futures.2023.103121

Pope, R. & Burnes, B. (2013) A model of organisational dysfunction in the NHS. Journal of Health Organization and Management 27 (6), 676-697. doi:10.1108/JHOM-10-2012-0207

Rouchier, J. (2023) Presentation to SocSimFest 23 during session ‘How to do wrong using Social Simulaion – as a result of arrogance, laziness or ill intent’. https://cfpm.org/slides/JR-Epi+newTINA.pdf

Roy, B. (1996) Multicriteria methodology for decision analysis, Kluwer Academic Publishers.

Singh, S, Roy, D., Sinha, K., Parveen, S., Sharma G. & Joshic, G. (2020) Impact of COVID-19 and lockdown on mental health of children and adolescents: A narrative review with recommendations, Psychiatry Research. 2020 Nov; 293: 113429, 10.1016/j.psychres.2020.113429

Smith, I. (2007). Breaking the dysfunctional dynamics. In: Building a World-Class NHS. Palgrave Macmillan, London, pp. 132-177. doi:10.1057/9780230589704_5

Sun, Z., Lorscheid, I., Millington, J. D., Lauf, S., Magliocca, N. R., Groeneveld, J., Balbi, S., Nolzen, H., Müller, B., Schulze, J. & Buchmann, C. M. (2016) Simple or complicated agent-based models? A complicated issue. Environmental Modelling & Software 86, 56-67. doi:10.1016/j.envsoft.2016.09.006

Usta, J., Murr, H. & El-Jarrah, R. (2021) COVID-19 lockdown and the increased violence against women: understanding domestic violence during a pandemic. Violence and Gender 8 (3), 133-139. doi:10.1089/vio.2020.0069

Voinov, A. & Shugart, H. H. (2013) ‘Integronsters’, integral and integrated modeling. Environmental Modelling & Software 39, 149-158. doi:10.1016/j.envsoft.2012.05.014

Polhill, G. and Rouchier, J. (2023) Policy modelling requires a multi-scale, multi-criteria and diverse-framing approach. Review of Artificial Societies and Social Simulation, 31 Jul 2023. https://rofasss.org/2023/07/31/policy-modelling-necessitates-multi-scale-multi-criteria-and-a-diversity-of-framing

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Content

An Institute for Crisis Modelling (ICM) – Towards a resilience center for sustained crisis modeling capability

May 22, 2023 thesubmissionauthor Leave a comment

By Fabian Lorig^1*, Bart de Bruin², Melania Borit³, Frank Dignum⁴, Bruce Edmonds⁵, Sinéad M. Madden⁶, Mario Paolucci⁷, Nicolas Payette⁸, Loïs Vanhée⁴

*Corresponding author
1 Internet of Things and People Research Center, Malmö University, Sweden
2 Delft University of Technology, Netherlands
3 CRAFT Lab, Arctic University of Norway, Tromsø, Norway
4 Department of Computing Science, Umeå University, Sweden
5 Centre for Policy Modelling, Manchester Metropolitan University Business School, UK
6 School of Engineering, University of Limerick, Ireland
7 Laboratory of Agent Based Social Simulation, ISTC/CNR, Italy
8 Complex Human-Environmental Systems Simulation Laboratory, University of Oxford, UK

The Need for an ICM

Most crises and disasters do occur suddenly and hit the society while it is unprepared. This makes it particularly challenging to react quick to their occurrence, to adapt to the resulting new situation, to minimize the societal impact, and to recover from the disturbance. A recent example was the Covid-19 crisis, which revealed weak points of our crisis preparedness. Governments were trying to put restrictions in place to limit the spread of the virus while ensuring the well-being of the population and at the same time preserving economic stability. It quickly became clear that interventions which worked well in some countries did not seem to have the intended effect in other countries and the reason for this is that the success of interventions to a great extent depends on individual human behavior.

Agent-based Social Simulations (ABSS) explicitly model the behavior of the individuals and their interactions in the population and allow us to better understand social phenomena. Thus, ABSS are perfectly suited for investigating how our society might be affected by different crisis scenarios and how policies might affect the societal impact and consequences of these disturbances. Particularly during the Covid-19 crisis, a great number of ABSS have been developed to inform policy making around the globe (e.g., Dignum et al. 2020, Balkely et al. 2021, Lorig et al. 2021). However, weaknesses in creating useful and explainable simulations in a short time also became apparent and there is still a lack of consistency to be better prepared for the next crisis (Squazzoni et al. 2020). Especially, ABSS development approaches are, at this moment, more geared towards simulating one particular situation and validating the simulation using data from that situation. In order to be prepared for a crisis, instead, one needs to simulate many different scenarios for which data might not yet be available. They also typically need a more interactive interface where stake holders can experiment with different settings, policies, etc.

For ABSS to become an established, reliable, and well-esteemed method for supporting crisis management, we need to organize and consolidate the available competences and resources. It is not sufficient to react once a crisis occurs but instead, we need to proactively make sure that we are prepared for future disturbances and disasters. For this purpose, we also need to systematically address more fundamental problems of ABSS as a method of inquiry and particularly consider the specific requirements for the use of ABSS to support policy making, which may differ from the use of ABSS in academic research. We therefore see the need for establishing an Institute for Crisis Modelling (ICM), a resilience center to ensure sustained crisis modeling capability.

The vision of starting an Institute for Crisis Modelling was the result of the discussions and working groups at the Lorentz Center workshop on “Agent Based Simulations for Societal Resilience in Crisis Situations” that took place in Leiden, Netherlands from 27 February to 3 March 2023**.

Vision of the ICM

“To have tools suitable to support policy actors in situations that are of
big uncertainty, large consequences, and dependent on human behavior.”

The ICM consists of a taskforce for quickly and efficiently supporting policy actors (e.g., decision makers, policy makers, policy analysts) in situations that are of big uncertainty, large consequences, and dependent on human behavior. For this purpose, the taskforce consists of a larger (informal) network of associates that contribute with their knowledge, skills, models, tools, and networks. The group of associates is composed of a core group of multidisciplinary modeling experts (ranging from social scientists and formal modelers to programmers) as well as of partners that can contribute to specific focus areas (like epidemiology, water management, etc.). The vision of ICM is to consolidate and institutionalize the use of ABSS as a method for crisis management. Although physically ABSS competences may be distributed over a variety of universities, research centers, and other institutions, the ICM serves as a virtual location that coordinates research developments and provides a basic level of funding and communication channel for ABSS for crisis management. This does not only provide policy actors with a single point of contact, making it easier for them to identify who to reach when simulation expertise is needed and to develop long-term trust relationships. It also enables us to jointly and systematically evolve ABSS to become a valuable and established tool for crisis response. The center combines all necessary resources, competences, and tools to quickly develop new models, to adapt existing models, and to efficiently react to new situations.

To achieve this goal and to evolve and establish ABSS as a valuable tool for policy makers in crisis situations, research is needed in different areas. This includes the collection, development, critical analysis, and review of fundamental principles, theories, methods, and tools used in agent-based modeling. This also includes research on data handling (analysis, sharing, access, protection, visualization), data repositories, ontologies, user-interfaces, methodologies, documentation, and ethical principles. Some of these points are concisely described in (Dignum, 2021, Ch. 14 and 15).

The ICM shall be able to provide a wide portfolio of models, methods, techniques, design patterns, and components required to quickly and effectively facilitate the work of policy actors in crisis situations by providing them with adequate simulation models. For the purpose of being able to provide specialized support, the institute will coordinate the human effort (e.g., the modelers) and have specific focus areas for which expertise and models are available. This might be, for instance, pandemics, natural disasters, or financial crises. For each of these focus areas, the center will develop different use cases, which ensures and facilitates rapid responses due to the availability of models, knowledge, and networks.

Objectives of the ICM

To achieve this vision, there are a series of objectives that a resilience center for sustained crisis modeling capability in crisis situations needs to address:

1) Coordinate and promote research

Providing quick and appropriate support for policy actors in crisis situations requires not only a profound knowledge on existing models, methods, tools, and theories but also the systematic development of new approaches and methodologies. This is to advance and evolve ABSS for being better prepared for future crises and will serve as a beacon for organizing the ABSS research oriented towards practical applications.

2) Enable trusted connections with policy actors

Sustainable collaborations and interactions with decision-makers and policy analysts as well as other relevant stakeholders is a great challenge in ABSS. Getting in contact with the right actors, “speaking the same language”, and having realistic expectations are only some of the common problems that need to be addressed. Thus, the ICM should not only connect to policy actors in times of crises, but have continuous interactions, provide sample simulations, develop use cases, and train the policy actors wherever possible.

3) Enable sustainability of the institute itself

Classic funding schemes are unfit for responding in crises, which require fast responses with always-available resources as well as the continuous build-up of knowledge, skills, network, and technological buildup requires long-term. Sustainable funding is needed that for enabling such a continuity, for which the IBM provides a demarked, unifying frame.

4) Actively maintain the network of associates

Maintaining a network of experts is challenging because it requires different competences and experiences. PhD candidates, for instance, might have a great practical experience in using different simulation frameworks, however, after their graduation, some might leave academia and others might continue to other positions where they do not have the opportunity to use their simulation expertise. Thus, new experts need to be acquired continuously to form a resilient and balanced network.

5) Inform policy actors

The most advanced and profound models cannot do any good in crisis situations in case of a lacking demand from policy actors. Many modelers perceive a certain hesitation from policy actors regarding the use of ABSS which might be due to them being unfamiliar with the potential benefits and use-cases of ABSS, lacking trust in the method itself, or simply due to a lack of awareness that ABSS actually exists. Hence, the center needs to educate policy makers and raise awareness as well as improve trust in ABSS.

6) Train the next generation of experts

To quickly develop suitable ABSS models in critical situations requires a variety of expertise. In addition to objective 4, the acquisition of associates, it is also of great importance to educate and train the next generation of experts. ABSS research is still a niche and not taught as an inherent part of the spectrum of methods of most disciplines. The center shall promote and strengthen ABSS education to ensure the training of the next generation of experts.

7) Engage the general public

Finally, the success of ABSS does not only depend on the trust of policy actors but also on how it is perceived by the general public. When developing interventions during the Covid-19 crisis and giving recommendations, the trust in the method was a crucial success factor. Also, developing realistic models requires the active participation of the general public.

Next steps

For ABSS to become a valuable and established tool for supporting policy actors in crisis situations, we are convinced that our efforts need to be institutionalized. This allows us to consolidate available competences, models, and tools as well as to coordinate research endeavors and the development of new approaches required to ensure a sustained crisis modeling capability.

To further pursue this vision, a Special Interest Group (SIG) on Building ResilienCe with Social Simulations (BRICSS) was established at the European Social Simulation Association (ESSA). Moreover, Special Tracks will be organized at the 2023 Social Simulation Conference (SSC) to bring together interested experts.

However, for this vision to become reality, the next steps towards establishing an Institute for Crisis Modelling consist of bringing together ambitious and competent associates as well as identifying core funding opportunities for the center. If the readers feel motivated to contribute in any way to this topic, they are encouraged to contact Frank Dignum, Umeå University, Sweden or any of the authors of this article.

Acknowledgements

This piece is a result of discussions at the Lorentz workshop on “Agent Based Simulations for Societal Resilience in Crisis Situations” at Leiden, NL in earlier this year! We are grateful to the organisers of the workshop and to the Lorentz Center as funders and hosts for such a productive enterprise. The final report of the workshop as well as more information can be found on the webpage of the Lorentz Center: https://www.lorentzcenter.nl/agent-based-simulations-for-societal-resilience-in-crisis-situations.html

References

Blakely, T., Thompson, J., Bablani, L., Andersen, P., Ouakrim, D. A., Carvalho, N., Abraham, P., Boujaoude, M.A., Katar, A., Akpan, E., Wilson, N. & Stevenson, M. (2021). Determining the optimal COVID-19 policy response using agent-based modelling linked to health and cost modelling: Case study for Victoria, Australia. Medrxiv, 2021-01. doi: 10.1101/2021.01.11.21249630

Dignum, F., Dignum, V., Davidsson, P., Ghorbani, A., van der Hurk, M., Jensen, M., Kammler C., Lorig, F., Ludescher, L.G., Melchior, A., Mellema, R., Pastrav, C., Vanhee, L. & Verhagen, H. (2020). Analysing the combined health, social and economic impacts of the coronavirus pandemic using agent-based social simulation. Minds and Machines, 30, 177-194. doi: 10.1007/s11023-020-09527-6

Dignum, F. (ed.). (2021) Social Simulation for a Crisis; Results and Lessons from Simulating the COVID-19 Crisis. Springer.

Lorig, Fabian, Johansson, Emil and Davidsson, Paul (2021) ‘Agent-Based Social Simulation of the Covid-19 Pandemic: A Systematic Review’ Journal of Artificial Societies and Social Simulation 24(3), 5. http://jasss.soc.surrey.ac.uk/24/3/5.html. doi: 10.18564/jasss.4601

Squazzoni, F. et al. (2020) ‘Computational Models That Matter During a Global Pandemic Outbreak: A Call to Action‘ Journal of Artificial Societies and Social Simulation 23(2), 10. http://jasss.soc.surrey.ac.uk/23/2/10.html. doi: 10.18564/jasss.4298

Lorig, F., de Bruin, B., Borit, M., Dignum, F., Edmonds, B., Madden, S.M., Paolucci, M., Payette, N. and Vanhée, L. (2023) An Institute for Crisis Modelling (ICM) – Towards a resilience center for sustained crisis modeling capability. Review of Artificial Societies and Social Simulation, 22 May 2023. https://rofasss.org/2023/05/22/icm

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Content

A Tale of Three Pandemic Models: Lessons Learned for Engagement with Policy Makers Before, During, and After a Crisis

May 15, 2023 thesubmissionauthor Leave a comment

By Emil Johansson^1,2, Vittorio Nespeca³, Mikhail Sirenko⁴, Mijke van den Hurk⁵, Jason Thompson⁶, Kavin Narasimhan⁷, Michael Belfrage^{1, 2}, Francesca Giardini⁸, and Alexander Melchior^5,9

Department of Computer Science and Media Technology, Malmö University, Sweden
Internet of Things and People Research Center, Malmö University, Sweden
Computational Science Lab, University of Amsterdam, The Netherlands
Faculty of Technology, Policy and Management, Delft University of Technology, The Netherlands
Department of Information and Computing Sciences, Utrecht University, The Netherlands
Transport, Health and Urban Design Research Lab, The University of Melbourne, Australia
Centre for Research in Social Simulation, University of Surrey, United Kingdom
Department of Sociology & Agricola School for Sustainable Development, University of Groningen, The Netherlands
Ministry of Economic Affairs and Climate Policy and Ministry of Agriculture, Nature and Food Quality, The Netherlands

Motivation

Pervasive and interconnected crises such as the COVID-19 pandemic, global energy shortages, geopolitical conflicts, and climate change have shown how a stronger collaboration between science, policy, and crisis management is essential to foster societal resilience. As modellers and computational social scientists we want to help. Several cases of model-based policy support have shown the potential of using modelling and simulation as tools to prepare for, learn from (Adam and Gaudou, 2017), and respond to crises (Badham et al., 2021). At the same time, engaging with policy-makers to establish effective crisis-management solutions remains a challenge for many modellers due to lacking forums that promote and help develop sustained science-policy collaborations. Equally challenging is to find ways to provide effective solutions under changing circumstances, as it is often the case with crises.

Despite the existing guidance regarding how modellers can engage with policy makers e.g. (Vennix, 1996; Voinov and Bousquet, 2010), this guidance often does not account for the urgency that characterizes crisis response. In this article, we tell the stories of three different models developed during the COVID-19 pandemic in different parts of the world. For each of the models, we draw key lessons for modellers regarding how to engage with policy makers before, during, and after crises. Our goal is to communicate the findings from our experiences to modellers and computational scientists who, like us, want to engage with policy makers to provide model-based policy and crisis management support. We use selected examples from Kurt Vonnegut’s 2004 lecture on ‘shapes of stories’ alongside analogy with Lewis Carroll’s Alice In Wonderland as inspiration for these stories.

Boy Meets Girl (Too Late)

A Social Simulation On the Corona Crisis’ (ASSOCC) tale

The perfect love story between social modellers and stakeholders would be they meet (pre-crisis), build a trusting foundation and then, when a crisis hits, they work together as a team, maybe have some fight, but overcome the crisis together and have a happily ever after.

In the case of the ASSOCC project, we as modellers met our stakeholders too late, (i.e., while we were already in the middle of the COVID-19 crisis). The stakeholders we aimed for had already met their ‘boy’: Epidemiological modellers. For them, we were just one of the many scientists showing new models and telling them that ours should be looked at. Although, for example, our model showed that using a track and tracing-app would not help reduce the rate of new COVID-19 infections (as turned out to be the case), our psychological and social approach was novel for them. It was not the right time to explain the importance of integrating these kinds of concepts in epidemiological models, so without this basic trust, they were reluctant to work with us.

The moral of our story is that not only should we invest in a (working) relationship during non-crisis times to get the stakeholders on board during a crisis, such an approach would be helpful for us modelers too. For example, we integrated both social and epidemiological models within the ASSOCC project. We wanted to validate our model with that used by Oxford University. However, our model choices were not compatible with this type of validation. Had we been working with these types of researchers before a pandemic, we could have built a proper foundation for validation.

So, our biggest lesson learned is the importance of having a good relationship with stakeholders before a crisis hits, when there is time to get into social models and show the advantages of using these. When you invest in building and consolidating this relationship over time, we promise a happily ever after for every social modeler and stakeholder (until the next crisis hits).

Modeller’s Adventures in Wonderland

A Health Emergency Response in Interconnected Systems (HERoS) tale

If you are a modeler, you are likely to be curious and imaginative, like Alice from “Alice’s Adventures in Wonderland.” You like to think about how the world works and make models that can capture these sometimes weird mechanisms. We are the same. When Covid came, we made a model of a city to understand how its citizens would behave.

But there is more. When Alice first saw the White Rabbit, she found him fascinating. A rabbit with a pocket watch which is too late, what could be more interesting? Similarly, our attention got caught by policymakers who wear waistcoats, who are always busy but can bring change. They must need a model that we made! But why are they running away? Our model is so helpful, just let us explain! Or maybe our model is not good enough?

Yes, we fell down deep into a rabbit hole. Our first encounter with a policymaker didn’t result in a happy “yes, let’s try your model out.” However, we kept knocking on doors. How many did Alice try? But alright, there is one. It seems too tiny. We met with a group of policymakers but had only 10 minutes to explain our large-scale data-driven agent-based-like model. How can we possibly do that? Drink from a “Drink me” bottle, which will make our presentation smaller! Well, that didn’t help. We rushed over all the model complexities too fast and got applause, but that’s it. Ok, we have the next one, which will last 1 hour. Quickly! Eat an “Eat me” cake that will make the presentation longer! Oh, too many unnecessary details this time. To the next venue!

We are in the garden. The garden of crisis response. And it is full of policymakers: Caterpillar, Duchess, Cheshire Cat and Mad Hatter. They talk riddles: “We need to consult with the Head of Paperclip Optimization and Supply Management,” want different things: “Can you tell us what will be the impact of a curfew. Hmm, yesterday?” and shift responsibility from one to another. Thankfully there is no Queen of Hearts who would order to behead us.

If the world of policymaking is complex, then the world of policymaking during the crisis is a wonderland. And we all live in it. We must overgrow our obsession with building better models, learn about its fuzzy inhabitants, and find a way to instead work together. Constant interaction and a better understanding of each other’s needs must be at the centre of modeler-policymaker relations.

“But I don’t want to go among mad people,” Alice remarked.

“Oh, you can’t help that,” said the Cat: “we’re all mad here. I’m mad. You’re mad.”

“How do you know I’m mad?” said Alice.

“You must be,” said the Cat, “or you wouldn’t have come here.”
Lewis Carroll, Alice in Wonderland

Cinderella – A city’s tale

Everyone thought Melbourne was just too ugly to go to the ball…..until a little magic happened.

Once upon a time, the bustling Antipodean city of Melbourne, Victoria found itself in the midst of a dark and disturbing period. While all other territories in the great continent of Australia had ridded themselves of the dreaded COVID-19 virus, it was itself, besieged. Illness and death coursed through the land.

Shunned, the city faced scorn and derision. It was dirty. Its sisters called it a “plague state” and the people felt great shame and sadness as their family, friends and colleagues continued to fall to the virus. All they wanted was a chance to rejoin their families and countryfolk at the ball. What could they do?

Though downtrodden, the kind-hearted and resilient residents of Melbourne were determined to regain control over their lives. They longed for a glimmer of sunshine on these long, gloomy days – a touch of magic, perhaps? They turned to their embattled leaders for answers. Where was their Fairy Godmother now?

In this moment of despair, a group of scientists offered a gift in the form of a powerful agent-based model that was running on a supercomputer. This model, the scientists said, might just hold the key to transforming the fate of the city from vanquished to victor (Blakely et al., 2020). What was this strange new science? This magical black box?

Other states and scientists scoffed. “You can never achieve this!”, they said. “What evidence do you have? These models are not to be trusted. Such a feat as to eliminate COVID-19 at this scale has never been done in the history of the world!” But what of it? Why should history matter? Quietly and determinedly, the citizens of Melbourne persisted. They doggedly followed the plan.

Deep down, even the scientists knew it was risky. People’s patience and enchantment with the mystical model would not last forever. Still, this was Melbourne’s only chance. They needed to eliminate the virus so it would no longer have a grip on their lives. The people bravely stuck to the plan and each day – even when schools and businesses began to re-open – the COVID numbers dwindled from what seemed like impossible heights. Each day they edged down…

and down…

and down…until…

Finally! As the clock struck midnight, the people of Melbourne achieved the impossible: they had defeated COVID-19 by eliminating transmission. With the help of the computer model’s magic, illness and death from the virus stopped. Melbourne had triumphed, emerging stronger and more united than ever before (Thompson et al., 2022a).

From that day forth, Melbourne was internationally celebrated as a shining example of resilience, determination, and the transformative power of hope. Tens of thousands of lives were saved – and after enduring great personal and community sacrifice, its people could once again dance at the ball.

But what was the fate of the scientists and the model? Did such an experience change the way agent-based social simulation was used in public health? Not really. The scientists went back to their normal jobs and the magic of the model remained just that – magic. Its influence vanished like fairy dust on a warm Summer’s evening.

Even to this day the model and its impact largely remains a mystery (despite over 10,000 words of ODD documentation). Occasionally, policy-makers or researchers going about their ordinary business might be heard to say, “Oh yes, the model. The one that kept us inside and ruined the economy. Or perhaps it was the other way around? I really can’t recall – it was all such a blur. Anyway, back to this new social problem – Shall we attack it with some big data and ML techniques?”.

The fairy dust has vanished but the concrete remains.

And in fairness, while agent-based social simulation remains mystical and our descriptions opaque, we cannot begrudge others for ever choosing concrete over dust (Thompson et al, 2022b).

Conclusions

So what is the moral of these tales? We consolidate our experiences into these main conclusions:

No connection means no impact. If modellers wish for their models to be useful before, during or after a crisis, then it is up to them to start establishing a connection and building trust with policymakers.
The window of opportunity for policy modelling during crises can be narrow, perhaps only a matter of days. Capturing it requires both that we can supply a model within the timeframe (impossible as it may appear) and that our relationship with stakeholders is already established.
Engagement with stakeholders requires knowledge and skills that might be too much to ask of modelers alone, including project management, communication with individuals without a technical background, and insight into the policymaking process.
Being useful only sometimes means being excellent. A good model is one that is useful. By investing more in building relationships with policymakers and learning about each other, we have a bigger chance of providing the needed insight. Such a shift, however, is radical and requires us to give up our obsession with the models and engage with the fuzziness of the world around us.
If we cannot communicate our models effectively, we cannot expect to build trust with end-users over the long term, whether they be policy-makers or researchers. Individual models – and agent-based social simulation in general – needs better understanding that can only be achieved through greater transparency and communication, however that is achieved.

As taxing, time-consuming and complex as the process of making policy impact with simulation models might be, it is very much a fight worth fighting; perhaps even more so during crises. Assuming our models would have a positive impact on the world, not striving to make this impact could be considered admitting defeat. Making models useful to policymakers starts with admitting the complexity of their environment and willingness to dedicate time and effort to learn about it and work together. That is how we can pave the way for many more stories with happy endings.

Acknowledgements

References

Adam, C. and Gaudou, B. (2017) ‘Modelling Human Behaviours in Disasters from Interviews: Application to Melbourne Bushfires’ Journal of Artificial Societies and Social Simulation 20(3), 12. http://jasss.soc.surrey.ac.uk/20/3/12.html. doi: 10.18564/jasss.3395

Badham, J., Barbrook-Johnson, P., Caiado, C. and Castellani, B. (2021) ‘Justified Stories with Agent-Based Modelling for Local COVID-19 Planning’ Journal of Artificial Societies and Social Simulation 24 (1) 8 http://jasss.soc.surrey.ac.uk/24/1/8.html. doi: 10.18564/jasss.4532

Crammond, B. R., & Kishore, V. (2021). The probability of the 6‐week lockdown in Victoria (commencing 9 July 2020) achieving elimination of community transmission of SARS‐CoV‐2. The Medical Journal of Australia, 215(2), 95-95. doi:10.5694/mja2.51146

Thompson, J., McClure, R., Blakely, T., Wilson, N., Baker, M. G., Wijnands, J. S., … & Stevenson, M. (2022). Modelling SARS‐CoV‐2 disease progression in Australia and New Zealand: an account of an agent‐based approach to support public health decision‐making. Australian and New Zealand Journal of Public Health, 46(3), 292-303. doi:10.1111/1753-6405.13221

Thompson, J., McClure, R., Scott, N., Hellard, M., Abeysuriya, R., Vidanaarachchi, R., … & Sundararajan, V. (2022). A framework for considering the utility of models when facing tough decisions in public health: a guideline for policy-makers. Health Research Policy and Systems, 20(1), 1-7. doi:10.1186/s12961-022-00902-6

Voinov, A., & Bousquet, F. (2010). Modelling with stakeholders. Environmental modelling & software, 25(11), 1268-1281. doi:10.1016/j.envsoft.2010.03.007

Vennix, J.A.M. (1996). Group Model Building: Facilitating Team Learning Using System Dynamics. Wiley.

Vonnegut, K. (2004). Lecture to Case College. https://www.youtube.com/watch?v=4_RUgnC1lm8

Johansson,E., Nespeca, V., Sirenko, M., van den Hurk, M., Thompson, J., Narasimhan, K., Belfrage, M., Giardini, F. and Melchior, A. (2023) A Tale of Three Pandemic Models: Lessons Learned for Engagement with Policy Makers Before, During, and After a Crisis. Review of Artificial Societies and Social Simulation, 15 Mar 2023. https://rofasss.org/2023/05/15/threepandemic

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Content

Towards an Agent-based Platform for Crisis Management

May 10, 2023 thesubmissionauthor Leave a comment

By Christian Kammler¹, Maarten Jensen¹, Rajith Vidanaarachchi² Cezara Păstrăv¹

Department of Computer Science, Umeå University, Sweden
Transport, Health, and Urban Design (THUD)
Research Lab, The University of Melbourne, Australia

“Always code as if the guy who ends up maintaining your code will be a violent psychopath who knows where you live.” — John Woods

1 Introduction

Agent-based modelling can be a valuable tool for gaining insight into crises [3], both, during and before to increase resilience. However, in the current state of the art, the models have to build up from scratch which is not well suitable for a crisis situation as it hinders quick responses. Consequently, the models do not play the central supportive role that they could. Not only is it hard to compare existing models (given the absence of existing standards) and asses their quality, but also the most widespread toolkits, such as Netlogo [6], MESA (Python) [4], Repast (Java) [1,5], or Agents.jl (Julia) [2], are specific for the modelling field and lack the platform support necessary to empower policy makers to use the model (see Figure 1).

Fig. 1. Platform in the middle as a connector between the code and the model and interaction point for the user. It must not require any expert knowledge.

While some of these issues are systemic within the field of ABM (Agent-Based Modelling) itself, we aim to alleviate some of them in this particular context by using a platform purpose-built for developing and using ABM in a crisis. To do so, we view the problem through a multi-dimensional space which is as follows (consisting of the dimensions A-F):

A: Back-end to front-end interactivity
B: User and stakeholder levels
– Social simulators to domain experts to policymakers
– Skills and expertise in coding, modelling and manipulating a model
C: Crisis levels (Risk, Crisis, Resilience – also identified as – Pre Crisis, In Crisis, Post Crisis)
D: Language specific to language independent
E: Domain specific to domain-independent (e.g.: flooding, pandemic, climate change, )
F: Required iteration level (Instant, rapid, slow)

A platform can now be viewed as a vector within this space. While all of these axes require in-depth research (for example in terms of correlation or where existing platforms fit), we chose to focus on the functionalities we believe would be the most relevant in ABM for crises.

2 Rapid Development

During a crisis, time is compressed, and fast iterations are necessary (mainly focusing on axes C and F), making instant and rapid/fast iterations necessary while slow iterations are not suitable. As the crisis develops, the model may need to be adjusted to quickly absorb new data, actors, events, and response strategies, leading to new scenarios that need to be modelled and simulated. In this environment, models need to be built with reusability and rapid versioning in mind from the beginning, otherwise every new change makes the model more unstable and less trustworthy.

While a suite of best practices exists in general Software Development, they are not widely used in the agent-based modelling community. The platform needs a coding environment that favors modular reusable code, easy storage and sharing of such modules in well-organized libraries and makes it easy to integrate existing modules with new code.

Having this modularity is not only helping with the right side of Figure 1, we can also use it to help with the left side of the Figure at the same time. Meaning that the conceptual model can be part of the respective module, allowing to quickly determine if a module is relevant and understanding what the module is doing. Furthermore, it can be used to create a top-level drag and drop like model building environment to allow for rapid changes without having to write code (given that we take of the interface properly).

Having the code and the conceptual model together would also lower the effort required to review these modules. The platform can further help with this task by keeping track of which modules have been reviewed, and with versioning of the modules, as they can be annotated accordingly. It has to be noted however,

that such as system does not guarantee a trustworthy model, even though it might be up to date in terms of versioning.

3 Model transparency

Another key factor we want to focus on is the stakeholder dimension (axis B). These people are not experts in terms of models, mainly the left side of Figure 1, and thus need extensive support to be empowered to use the simulation in a – for them – meaningful way. While for the visualization side (the how? ) we can use insights from Data Visualization, for the why side it is not that easy.

In a crisis, it is crucial to quickly determine why the model behaves in a certain way in order to interpret the results. Here, the platform can help by offering tools to build model narratives (at agent, group, or whole population level), to detect events and trends, and to compare model behavior between runs. We can take inspiration from the larger software development field for a few useful ideas on how to visually track model elements, log the behavior of model elements, or raise flags when certain conditions or events are detected. However, we also have to be careful here, as we easily move towards the technical solution side and away from the stakeholder and policy maker. Therefore, more research has to be done on what support policy makers actually need. An avenue here can be techniques from data story-telling.

4 The way forward

What this platform will look like depends on the approaches we take going forward. We think that the following two questions are central (also to prompt further research):

What are relevant roles that can be identified for a platform?
Given a role for the platform, where should it exist within the space de- scribed, and what attributes/characteristics should it have?

While these questions are key to identify whether or not existing platforms can be extended and shaped in the way we need them or if we need to build a sandbox from scratch, we strongly advocate or an open source approach. An open source approach can not only help to allow for the use of the range of expertise spread across the field, but also alleviate some of the trust challenges. One of the main challenges is that a trustworthy, well-curated model base with different modules does not yet exist. As such, the platform should aim first to aid in building this shared resource and add more related functionality as it becomes relevant. As for model tracking tools, we should aim for simple tools first and build more complex functionality on top of them later.

A starting point can be to build modules for existing crises, such as earth- quakes or floods where it is possible to pre-identify most of the modelling needs, the level of stakeholder engagement, the level of policymaker engagement, etc.

With this we can establish the process of open-source modelling and learn how to integrate new knowledge quickly, and be potentially better prepared for unknown crises in the future.

Acknowledgements

References

Collier, N., North, M.: Parallel agent-based simulation with repast for high per- formance computing. SIMULATION 89(10), 1215–1235 (2013), https://doi.org/10. 1177/0037549712462620
Datseris, G., Vahdati, A.R., DuBois, T.C.: Agents.jl: a performant and feature-full agent-based modeling software of minimal code complexity. SIMULATION 0(0), 003754972110688 (2022), https://doi.org/10.1177/00375497211068820
Dignum, F. (ed.): Social Simulation for a Crisis: Results and Lessons from Simulating the COVID-19 Crisis. Springer International Publishing, Cham (2021)
Kazil, J., Masad, D., Crooks, A.: Utilizing python for agent-based modeling: The mesa framework. In: Thomson, R., Bisgin, H., Dancy, C., Hyder, A., Hussain, M. (eds.) Social, Cultural, and Behavioral Modeling. pp. 308–317. Springer Interna- tional Publishing, Cham (2020)
North, M.J., Collier, N.T., Ozik, J., Tatara, E.R., Macal, C.M., Bragen, M., Sydelko, P.: Complex adaptive systems modeling with Repast Simphony. Complex Adaptive Systems Modeling 1(1), 3 (March 2013), https://doi.org/10.1186/2194-3206-1-3
Wilensky, U.: Netlogo. http://ccl.northwestern.edu/netlogo/, Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999), http://ccl.northwestern.edu/netlogo/

Kammler, C., Jensen, M., Vidanaarachchi, R. and Păstrăv, C. (2023) Towards an Agent-based Platform for Crisis Management. Review of Artificial Societies and Social Simulation, 10 May 2023. https://rofasss.org/2023/05/10/abm4cm

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Meta, Model Reproduction Reports, review

RofASSS to encourage reproduction reports and reviews of old papers&books

February 8, 2023 someeditorialcontent 1 Comment

Reproducing simulation models is essential for verifying them and critiquing them. This involves a lot more work than one would think (Axtell & al. 1996) and can reveal surprising flaws, even in the simplest of models (e.g. Edmonds & Hales 2003). Such reproduction is especially vital if the model outcomes are likely to affect people’s lives (Chattoe-Brown & al. 2021).

Whilst substantial pieces of work – where there is extensive analysis or extension – can be submitted to JASSS/CMOT, some such reports might be much simpler and not justify a full journal paper. Thus RofASSS has decided to encourage researchers to submit reports of reproductions here – however simple or complicated.

Similarly, JASSS, CMOT etc. do publish book reviews, but these tend to be of recent books. Although new books are of obvious interest to those at the cutting edge of research, it often happens that important papers & books are forgotten or overlooked. At RofASSS we would like to encourage reviews of any relevant book or paper, however old.

References

Axtell, R., Axelrod, R., Epstein, J. M., & Cohen, M. D. (1996). Aligning simulation models: A case study and results. Computational & Mathematical Organization Theory, 1, 123-141. DOI: 10.1007/BF01299065

Edmonds, B., & Hales, D. (2003). Replication, replication and replication: Some hard lessons from model alignment. Journal of Artificial Societies and Social Simulation, 6(4), 11. https://jasss.soc.surrey.ac.uk/6/4/11.html

Chattoe-Brown, E. Gilbert, N., Robertson, D. A. & Watts, C. (2021) Reproduction as a Means of Evaluating Policy Models: A Case Study of a COVID-19 Simulation. medRxiv 2021.01.29.21250743; DOI: 10.1101/2021.01.29.21250743

Content

Reply to Frank Dignum

November 10, 2021 thesubmissionauthor Leave a comment

By Edmund Chattoe-Brown

This is a reply to Frank Dignum’s reply (about Edmund Chattoe-Brown’s review of Frank’s book)

As my academic career continues, I have become more and more interested in the way that people justify their modelling choices, for example, almost every Agent-Based Modeller makes approving noises about validation (in the sense of comparing real and simulated data) but only a handful actually try to do it (Chattoe-Brown 2020). Thus I think two specific statements that Frank makes in his response should be considered carefully:

“… we do not claim that we have the best or only way of developing an Agent-Based Model (ABM) for crises.” Firstly, negative claims (“This is not a banana”) are not generally helpful in argument. Secondly, readers want to know (or should want to know) what is being claimed and, importantly, how they would decide if it is true “objectively”. Given how many models sprang up under COVID it is clear that what is described here cannot be the only way to do it but the question is how do we know you did it “better?” This was also my point about institutionalisation. For me, the big lesson from COVID was how much the automatic response of the ABM community seems to be to go in all directions and build yet more models in a tearing hurry rather than synthesise them, challenge them or test them empirically. I foresee a problem both with this response and our possible unwillingness to be self-aware about it. Governments will not want a million “interesting” models to choose from but one where they have externally checkable reasons to trust it and that involves us changing our mindset (to be more like climate modellers for example, Bithell & Edmonds 2020). For example, colleagues and I developed a comparison methodology that allowed for the practical difficulties of direct replication (Chattoe-Brown et al. 2021).
The second quotation which amplifies this point is: “But we do think it is an extensive foundation from which others can start, either picking up some bits and pieces, deviating from it in specific ways or extending it in specific ways.” Again, here one has to ask the right question for progress in modelling. On what scientific grounds should people do this? On what grounds should someone reuse this model rather than start their own? Why isn’t the Dignum et al. model built on another “market leader” to set a good example? (My point about programming languages was purely practical not scientific. Frank is right that the model is no less valid because the programming language was changed but a version that is now unsupported seems less useful as a basis for the kind of further development advocated here.)

I am not totally sure I have understood Frank’s point about data so I don’t want to press it but my concern was that, generally, the book did not seem to “tap into” relevant empirical research (and this is a wider problem that models mostly talk about other models). It is true that parameter values can be adjusted arbitrarily in sensitivity analysis but that does not get us any closer to empirically justified parameter values (which would then allow us to attempt validation by the “generative methodology”). Surely it is better to build a model that says something about the data that exists (however imperfect or approximate) than to rely on future data collection or educated guesses. I don’t really have the space to enumerate the times the book said “we did this for simplicity”, “we assumed that” etc. but the cumulative effect is quite noticeable. Again, we need to be aware of the models which use real data in whatever aspects and “take forward” those inputs so they become modelling standards. This has to be a collective and not an individualistic enterprise.

References

Bithell, M. and Edmonds, B. (2020) The Systematic Comparison of Agent-Based Policy Models – It’s time we got our act together!. Review of Artificial Societies and Social Simulation, 11th May 2021. https://rofasss.org/2021/05/11/SystComp/

Chattoe-Brown, E. (2020) A Bibliography of ABM Research Explicitly Comparing Real and Simulated Data for Validation. Review of Artificial Societies and Social Simulation, 12th June 2020. https://rofasss.org/2020/06/12/abm-validation-bib/

Chattoe-Brown, E. (2021) A review of “Social Simulation for a Crisis: Results and Lessons from Simulating the COVID-19 Crisis”. Journal of Artificial Society and Social Simulation. 24(4). https://www.jasss.org/24/4/reviews/1.html

Chattoe-Brown, E., Gilbert, N., Robertson, D. A., & Watts, C. J. (2021). Reproduction as a Means of Evaluating Policy Models: A Case Study of a COVID-19 Simulation. medRxiv 2021.01.29.21250743; DOI: https://doi.org/10.1101/2021.01.29.21250743

Dignum, F. (2020) Response to the review of Edmund Chattoe-Brown of the book “Social Simulations for a Crisis”. Review of Artificial Societies and Social Simulation, 4th Nov 2021. https://rofasss.org/2021/11/04/dignum-review-response/

Dignum, F. (Ed.) (2021) Social Simulation for a Crisis: Results and Lessons from Simulating the COVID-19 Crisis. Springer. DOI:10.1007/978-3-030-76397-8

Chattoe-Brown, E. (2021) Reply to Frank Dignum. Review of Artificial Societies and Social Simulation, 10th November 2021. https://rofasss.org/2021/11/10/reply-to-dignum/

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Content

Response to the review of Edmund Chattoe-Brown of the book “Social Simulations for a Crisis”

November 4, 2021 thesubmissionauthor Leave a comment

By Frank Dignum

This is a reply to a review in JASSS (Chattoe-Brown 2021) of (Dignum 2021).

Before responding to some of the specific concerns of Edmund I would like to thank him for the thorough review. I am especially happy with his conclusion that the book is solid enough to make it a valuable contribution to scientific progress in modelling crises. That was the main aim of the book and it seems that is achieved. I want to reiterate what we already remarked in the book; we do not claim that we have the best or only way of developing an Agent-Based Model (ABM) for crises. Nor do we claim that our simulations were without limitations. But we do think it is an extensive foundation from which others can start, either picking up some bits and pieces, deviating from it in specific ways or extending it in specific ways.

The concerns that are expressed by Edmund are certainly valid. I agree with some of them, but will nuance some others. First of all the concern about the fact that we seem to abandon the NetLogo implementation and move to Repast. This fact does not make the ABM itself any less valid! In itself it is also an important finding. It is not possible to scale such a complex model in NetLogo beyond around two thousand agents. This is not just a limitation of our particular implementation, but a more general limitation of the platform. It leads to the important challenge to get more computer scientists involved to develop platforms for social simulations that both support the modelers adequately and provide efficient and scalable implementations.

That the sheer size of the model and the results make it difficult to trace back the importance and validity of every factor on the results is completely true. We have tried our best to highlight the most important aspects every time. But, this leaves questions as to whether we make the right selection of highlighted aspects. As an illustration to this, we have been busy for two months to justify our results of the simulations of the effectiveness of the track and tracing apps. We basically concluded that we need much better integrated analysis tools in the simulation platform. NetLogo is geared towards creating one simulation scenario, running the simulation and analyzing the results based on a few parameters. This is no longer sufficient when we have a model with which we can create many scenarios and have many parameters that influence a result. We used R now to interpret the flood of data that was produced with every scenario. But, R is not really the most user friendly tool and also not specifically meant for analyzing the data from social simulations.

Let me jump to the third concern of Edmund and link it to the analysis of the results as well. While we tried to justify the results of our simulation on the effectiveness of the track and tracing app we compared our simulation with an epidemiological based model. This is described in chapter 12 of the book. Here we encountered the difference in assumed number of contacts per day a person has with other persons. One can take the results, as quoted by Edmund as well, of 8 or 13 from empirical work and use them in the model. However, the dispute is not about the number of contacts a person has per day, but what counts as a contact! For the COVID-19 simulations standing next to a person in the queue in a supermarket for five minutes can count as a contact, while such a contact is not a meaningful contact in the cited literature. Thus, we see that what we take as empirically validated numbers might not at all be the right ones for our purpose. We have tried to justify all the values of parameters and outcomes in the context for which the simulations were created. We have also done quite some sensitivity analyses, which we did not all report on just to keep the volume of the book to a reasonable size. Although we think we did a proper job in justifying all results, that does not mean that one can have different opinions on the value that some parameters should have. It would be very good to check the influence on the results of changes in these parameters. This would also progress scientific insights in the usefulness of complex models like the one we made!

I really think that an ABM crisis response should be institutional. That does not mean that one institution determines the best ABM, but rather that the ABM that is put forward by that institution is the result of a continuous debate among scientists working on ABM’s for that type of crisis. For us, one of the more important outcomes of the ASSOCC project is that we really need much better tools to support the types of simulations that are needed for a crisis situation. However, it is very difficult to develop these tools as a single group. A lot of the effort needed is not publishable and thus not valued in an academic environment. I really think that the efforts that have been put in platforms such as NetLogo and Repast are laudable. They have been made possible by some generous grants and institutional support. We argue that this continuous support is also needed in order to be well equipped for a next crisis. But we do not argue that an institution would by definition have the last word in which is the best ABM. In an ideal case it would accumulate all academic efforts as is done in the climate models, but even more restricted models would still be better than just having a thousand individuals all claiming to have a useable ABM while governments have to react quickly to a crisis.

The final concern of Edmund is about the empirical scale of our simulations. This is completely true! Given the scale and details of what we can incorporate we can only simulate some phenomena and certainly not everything around the COVID-19 crisis. We tried to be clear about this limitation. We had discussions about the Unity interface concerning this as well. It is in principle not very difficult to show people walking in the street, taking a car or a bus, etc. However, we decided to show a more abstract representation just to make clear that our model is not a complete model of a small town functioning in all aspects. We have very carefully chosen which scenarios we can realistically simulate and give some insights in reality from. Maybe we should also have discussed more explicitly all the scenarios that we did not run with the reasons why they would be difficult or unrealistic in our ABM. One never likes to discuss all the limitations of one’s labor, but it definitely can be very insightful. I have made up for this a little bit by submitting an to a special issue on predictions with ABM in which I explain in more detail, which should be the considerations to use a particular ABM to try to predict some state of affairs. Anyone interested to learn more about this can contact me.

To conclude this response to the review, I again express my gratitude for the good and thorough work done. The concerns that were raised are all very valuable to concern. What I tried to do in this response is to highlight that these concerns should be taken as a call to arms to put effort in social simulation platforms that give better support for creating simulations for a crisis.

References

Dignum, F. (Ed.) (2021) Social Simulation for a Crisis: Results and Lessons from Simulating the COVID-19 Crisis. Springer. DOI:10.1007/978-3-030-76397-8

Dignum, F. (2020) Response to the review of Edmund Chattoe-Brown of the book “Social Simulations for a Crisis”. Review of Artificial Societies and Social Simulation, 4th Nov 2021. https://rofasss.org/2021/11/04/dignum-review-response/

Content

The Systematic Comparison of Agent-Based Policy Models – It’s time we got our act together!

May 11, 2021 thesubmissionauthor 6 Comments

By Mike Bithell and Bruce Edmonds

Model Intercomparison

The recent Covid crisis has led to a surge of new model development and a renewed interest in the use of models as policy tools. While this is in some senses welcome, the sudden appearance of many new models presents a problem in terms of their assessment, the appropriateness of their application and reconciling any differences in outcome. Even if they appear similar, their underlying assumptions may differ, their initial data might not be the same, policy options may be applied in different ways, stochastic effects explored to a varying extent, and model outputs presented in any number of different forms. As a result, it can be unclear what aspects of variations in output between models are results of mechanistic, parameter or data differences. Any comparison between models is made tricky by differences in experimental design and selection of output measures.

If we wish to do better, we suggest that a more formal approach to making comparisons between models would be helpful. However, it appears that this is not commonly undertaken most fields in a systematic and persistent way, except for the field of climate change, and closely related fields such as pollution transport or economic impact modelling (although efforts are underway to extend such systematic comparison to ecosystem models – Wei et al., 2014, Tittensor et al., 2018⁠). Examining the way in which this is done for climate models may therefore prove instructive.

Model Intercomparison Projects (MIP) in the Climate Community

Formal intercomparison of atmospheric models goes back at least to 1989 (Gates et al., 1999)⁠ with the first atmospheric model inter-comparison project (AMIP), initiated by the World Climate Research Programme. By 1999 this had contributions from all significant atmospheric modelling groups, providing standardised time-series of over 30 model variables for one particular historical decade of simulation, with a standard experimental setup. Comparisons of model mean values with available data helped to reveal overall model strengths and weaknesses: no single model was best at simulation of all aspects of the atmosphere, with accuracy varying greatly between simulations. The model outputs also formed a reference base for further inter-comparison experiments including targets for model improvement and reduction of systematic errors, as well as a starting point for improved experimental design, software and data management standards and protocols for communication and model intercomparison. This led to AMIPII and, subsequently, to a series of Climate model inter-comparison projects (CMIP) beginning with CMIP I in 1996. The latest iteration (CMIP 6) is a collection of 23 separate model intercomparison experiments covering atmosphere, ocean, land surface, geo-engineering, and the paleoclimate. This collection is aimed at the upcoming 2021 IPCC process (AR6). Participating projects go through an endorsement process for inclusion, (a process agreed with modelling groups), based on 10 criteria designed to ensure some degree of coherence between the various models – a further 18 MIPS are also listed as currently active (https://www.wcrp-climate.org/wgcm-cmip/wgcm-cmip6). Groups contribute to a central set of common experiments covering the period 1850 to the near-present. An overview of the whole process can be found in (Eyring et al., 2016).

The current structure includes a set of three overarching questions covering the dynamics of the earth system, model systematic biases and understanding possible future change under uncertainty. Individual MIPS may build on this to address one or more of a set of 7 “grand science challenges” associated with the climate. Modelling groups agree to provide outputs in a standard form, obtained from a specified set of experiments under the same design, and to provide standardised documentation to go with their models. Originally (up to CMIP 5), outputs were then added to a central public repository for further analysis, however the output grew so large under CMIP6 that now the data is held dispersed over repositories maintained by separate groups.

Other Examples

Two further more recent examples of collective model development may also be helpful to consider.

Firstly, an informal network collating models across more than 50 research groups has already been generated as a result of the COVID crisis – the Covid Forecast Hub (https://covid19forecasthub.org). This is run by a small number of research groups collaborating with the US Centre for Disease Control and is strongly focussed on the epidemiology. Participants are encouraged to submit weekly forecasts, and these are integrated into a data repository and can be vizualized on the website – viewers can look at forward projections, along with associated confidence intervals and model evaluation scores, including those for an ensemble of all models. The focus on forecasts in this case arises out of the strong policy drivers for the current crisis, but the main point is that it is possible to immediately view measures of model performance and to compare the different model types: one clear message that rapidly becomes apparent is that many of the forward projections have 95% (and at some times, even 50%) confidence intervals for incident deaths that more than span the full range of the past historic data. The benefit of comparing many different models in this case is apparent, as many of the historic single-model projections diverge strongly from the data (and the models most in error are not consistently the same ones over time), although the ensemble mean tends to be better.

As a second example, one could consider the Psychological Science Accelerator (PSA: Moshontz et al 2018, https://psysciacc.org/). This is a collaborative network set up with the aim of addressing the “replication crisis” in psychology: many previously published results in psychology have proved problematic to replicate as a result of small or non-representative sampling or use of experimental designs that do not generalize well or have not been used consistently either within or across studies. The PSA seeks to ensure accumulation of reliable and generalizable evidence in psychological science, based on principles of inclusion, decentralization, openness, transparency and rigour. The existence of this network has, for example, enabled the reinvestigation of previous experiments but with much larger and less nationally biased samples (e.g. Jones et al 2021).

The Benefits of the Intercomparison Exercises and Collaborative Model Building

More specifically, long-term intercomparison projects help to do the following.

Build on past effort. Rather than modellers re-inventing the wheel (or building a new framework) with each new model project, libraries of well-tested and documented models, with data archives, including code and experimental design, would allow researchers to more efficiently work on new problems, building on previous coding effort
Aid replication. Focussed long term intercomparison projects centred on model results with consistent standardised data formats would allow new versions of code to be quickly tested against historical archives to check whether expected results could be recovered and where differences might arise, particularly if different modelling languages were being used
Help to formalize. While informal code archives can help to illustrate the methods or theoretical foundations of a model, intercomparison projects help to understand which kinds of formal model might be good for particular applications, and which can be expected to produce helpful results for given desired output measures
Build credibility. A continuously updated set of model implementations and assessment of their areas of competence and lack thereof (as compared with available datasets) would help to demonstrate the usefulness (or otherwise) of ABM as a way to represent social systems
Influence Policy (where appropriate). Formal international policy organisations such as the IPCC or the more recently formed IPBES are effective partly through an underpinning of well tested and consistently updated models. As yet it is difficult to see whether such a body would be appropriate or effective for social systems, as we lack the background of demonstrable accumulated and well tested model results.

Lessons for ABM?

What might we be able to learn from the above, if we attempted to use a similar process to compare ABM policy models?

In the first place, the projects started small and grew over time: it would not be necessary, for example, to cover all possible ABM applications at the outset. On the other hand, the latest CMIP iterations include a wide range of different types of model covering many different aspects of the earth system, so that the breadth of possible model types need not be seen as a barrier.

Secondly, the climate inter-comparison project has been persistent for some 30 years – over this time many models have come and gone, but the history of inter-comparisons allows for an overview of how well these models have performed over time – data from the original AMIP I models is still available on request, supporting assessments concerning long-term model improvement.

Thirdly, although climate models are complex – implementing a variety of different mechanisms in different ways – they can still be compared by use of standardised outputs, and at least some (although not necessarily all) have been capable of direct comparison with empirical data.

Finally, an agreed experimental design and public archive for documentation and output that is stable over time is needed; this needs to be done via a collective agreement among the modelling groups involved so as to ensure a long-term buy-in from the community as a whole, so that there is a consistent basis for long-term model development, building on past experience.

The need for aligning or reproducing ABMs has long been recognised within the community (Axtell et al. 1996; Edmonds & Hales 2003), but on a one-one basis for verifying the specification of models against their implementation, although (Hales et al. 2003) discusses a range of possibilities. However, this is far from a situation where many different models of basically the same phenomena are systematically compared – this would be a larger scale collaboration lasting over a longer time span.

The community has already established a standardised form of documentation in the ODD protocol. Sharing of model code is also becoming routine, and can be easily achieved through COMSES, Github or similar. The sharing of data in a long-term archive may require more investigation. As a starting project COVID-19 provides an ideal opportunity for setting up such a model inter-comparison project – multiple groups already have running examples, and a shared set of outputs and experiments should be straightforward to agree on. This would potentially form a basis for forward looking experiments designed to assist with possible future pandemic problems, and a basis on which to build further features into the existing disease-focussed modelling, such as the effects of economic, social and psychological issues.

Additional Challenges for ABMs of Social Phenomena

Nobody supposes that modelling social phenomena is going to have the same set of challenges that climate change models face. Some of the differences include:

The availability of good data. Social science is bedevilled by a paucity of the right kind of data. Although an increasing amount of relevant data is being produced, there are commercial, ethical and data protection barriers to accessing it and the data rarely concerns the same set of actors or events.
The understanding of micro-level behaviour. Whilst the micro-level understanding of our atmosphere is very well established, those of the behaviour of the most important actors (humans) is not. However, it may be that better data might partially substitute for a generic behavioural model of decision-making.
Agreement upon the goals of modelling. Although there will always be considerable variation in terms of what is wanted from a model of any particular social phenomena, a common core of agreed objectives will help focus any comparison and give confidence via ensembles of projections. Although the MIPs and Covid Forecast Hub are focussed on prediction, it may be that empirical explanation may be more important in other areas.
The available resources. ABM projects tend to be add-ons to larger endeavours and based around short-term grant funding. The funding for big ABM projects is yet to be established, not having the equivalent of weather forecasting to piggy-back on.
Persistence of modelling teams/projects. ABM tends to be quite short-term with each project developing a new model for a new project. This has made it hard to keep good modelling teams together.
Deep uncertainty. Whilst the set of possible factors and processes involved in a climate change model are well established, which social mechanisms need to be involved in any model of any particular social phenomena is unknown. For this reason, there is deep disagreement about the assumptions to be made in such models, as well as sharp divergence in outcome due to changes brought about by a particular mechanism but not included in a model. Whilst uncertainty in known mechanisms can be quantified, assessing the impact of those due to such deep uncertainty is much harder.
The sensitivity of the political context. Even in the case of Climate Change, where the assumptions made are relatively well understood and done on objective bases, the modelling exercise and its outcomes can be politically contested. In other areas, where the representation of people’s behaviour might be key to model outcomes, this will need even more care (Adoha & Edmonds 2017).

However, some of these problems were solved in the case of Climate Change as a result of the CMIP exercises and the reports they ultimately resulted in. Over time the development of the models also allowed for a broadening and updating of modelling goals, starting from a relatively narrow initial set of experiments. Ensuring the persistence of individual modelling teams is easier in the context of an internationally recognised comparison project, because resources may be easier to obtain, and there is a consistent central focus. The modelling projects became longer-term as individual researchers could establish a career doing just climate change modelling and importance of the work increasingly recognised. An ABM modelling comparison project might help solve some of these problems as the importance of its work is established.

Towards an Initial Proposal

The topic chosen for this project should be something where there: (a) is enough public interest to justify the effort, (b) there are a number of models with a similar purpose in mind being developed. At the current stage, this suggests dynamic models of COVID spread, but there are other possibilities, including: transport models (where people go and who they meet) or criminological models (where and when crimes happen).

Whichever ensemble of models is focussed upon, these models should be compared on a core of standard, with the same:

Start and end dates (but not necessarily the same temporal granularity)
Covering the same set of regions or cases
Using the same population data (though possibly enhanced with extra data and maybe scaled population sizes)
With the same initial conditions in terms of the population
Outputting a core of agreed measures (but maybe others as well)
Checked against their agreement against a core set of cases, with agreed data sets
Reported on in a standard format (though with a discussion section for further/other observations)
well documented and with code that is open access
Run a minimum of times with different random seeds

Any modeller/team that had a suitable model and was willing to adhere to the rules would be welcome to participate (commercial, government or academic) and these teams would collectively decide the rules, development and write any reports on the comparisons. Other interested stakeholder groups could be involved including professional/academic associations, NGOs and government departments but in a consultative role providing wider critique – it is important that the terms and reports from the exercise be independent or any particular interest or authority.

Conclusion

We call upon those who think ABMs have the potential to usefully inform policy decisions to work together, in order that the transparency and rigour of our modelling matches our ambition. Whilst model comparison exercises of the kind described are important for any simulation work, particular care needs to be taken when the outcomes can affect people’s lives.

References

Aodha, L. & Edmonds, B. (2017) Some pitfalls to beware when applying models to issues of policy relevance. In Edmonds, B. & Meyer, R. (eds.) Simulating Social Complexity – a handbook, 2nd edition. Springer, 801-822. (A version is at http://cfpm.org/discussionpapers/236)

Axtell, R., Axelrod, R., Epstein, J. M., & Cohen, M. D. (1996). Aligning simulation models: A case study and results. Computational & Mathematical Organization Theory, 1(2), 123-141. https://link.springer.com/article/10.1007%2FBF01299065

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., & Taylor, K. E. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development, 9(5), 1937–1958. https://doi.org/10.5194/gmd-9-1937-2016

Gates, W. L., Boyle, J. S., Covey, C., Dease, C. G., Doutriaux, C. M., Drach, R. S., Fiorino, M., Gleckler, P. J., Hnilo, J. J., Marlais, S. M., Phillips, T. J., Potter, G. L., Santer, B. D., Sperber, K. R., Taylor, K. E., & Williams, D. N. (1999). An Overview of the Results of the Atmospheric Model Intercomparison Project (AMIP I). In Bulletin of the American Meteorological Society (Vol. 80, Issue 1, pp. 29–55). American Meteorological Society. https://doi.org/10.1175/1520-0477(1999)080<0029:AOOTRO>2.0.CO;2

Hales, D., Rouchier, J., & Edmonds, B. (2003). Model-to-model analysis. Journal of Artificial Societies and Social Simulation, 6(4), 5. http://jasss.soc.surrey.ac.uk/6/4/5.html

Jones, B.C., DeBruine, L.M., Flake, J.K. et al. To which world regions does the valence–dominance model of social perception apply?. Nat Hum Behav 5, 159–169 (2021). https://doi.org/10.1038/s41562-020-01007-2

Moshontz, H. + 85 others (2018) The Psychological Science Accelerator: Advancing Psychology Through a Distributed Collaborative Network , 1(4) 501-515. https://doi.org/10.1177/2515245918797607

Tittensor, D. P., Eddy, T. D., Lotze, H. K., Galbraith, E. D., Cheung, W., Barange, M., Blanchard, J. L., Bopp, L., Bryndum-Buchholz, A., Büchner, M., Bulman, C., Carozza, D. A., Christensen, V., Coll, M., Dunne, J. P., Fernandes, J. A., Fulton, E. A., Hobday, A. J., Huber, V., … Walker, N. D. (2018). A protocol for the intercomparison of marine fishery and ecosystem models: Fish-MIP v1.0. Geoscientific Model Development, 11(4), 1421–1442. https://doi.org/10.5194/gmd-11-1421-2018

Wei, Y., Liu, S., Huntzinger, D. N., Michalak, A. M., Viovy, N., Post, W. M., Schwalm, C. R., Schaefer, K., Jacobson, A. R., Lu, C., Tian, H., Ricciuto, D. M., Cook, R. B., Mao, J., & Shi, X. (2014). The north american carbon program multi-scale synthesis and terrestrial model intercomparison project – Part 2: Environmental driver data. Geoscientific Model Development, 7(6), 2875–2893. https://doi.org/10.5194/gmd-7-2875-2014

Bithell, M. and Edmonds, B. (2020) The Systematic Comparison of Agent-Based Policy Models - It’s time we got our act together!. Review of Artificial Societies and Social Simulation, 11th May 2021. https://rofasss.org/2021/05/11/SystComp/

Content

Should the family size be used in COVID-19 vaccine prioritization strategy to prevent variants diffusion? A first investigation using a basic ABM

April 15, 2021 thesubmissionauthor Leave a comment

By Gianfranco Giulioni

Department of Philosophical, Pedagogical and Economic-Quantitative Sciences, University of Chieti-Pescara, Italy

(A contribution to the: JASSS-Covid19-Thread)

When writing this document, few countries have made significant progress in vaccinating their population while many others still move first steps.

Despite the importance of COVID-19 adverse effects on society, there seems to be too little debate on the best option for progressing the vaccination process after the front-line healthcare personnel has been immunized.

The overall adopted strategies in the front-runner countries prioritize people using their health fragility, and age. For example, this strategy’s effectiveness is supported by Bubar et al. (2021), who provide results based on a detailed age-stratified Susceptible, Exposed, Infectious, Recovered (SEIR) model.

During the Covid infection outbreak, the importance of families in COVID diffusion was stressed by experts and media. This observation motivates the present effort, which investigates if considering family size among the vaccine prioritization strategy can have a role.

This document describes an ABM model developed with the intent of analyzing the question. The model is basic and has the essentials features to investigate the issue.

As highlighted by Squazzoni et al. (2020) a careful investigation of pandemics requires the cooperation of many scientists from different disciplines. To ease this cooperation and to the aim of transparency (Barton et al. 2020), the code is made publicly available to allow further developments and accurate parameters calibration to those who might be interested. (https://github.com/gfgprojects/abseir_family)

The following part of the document will sketch the model functioning and provide some considerations on families’ effects on vaccination strategy.

Brief Model Description

The ABSEIR-family model code is written in Java, taking advantage of the Repast Simphony modeling system (https://repast.github.io/).

Figure 1 gives an overview of the current development state of the model core classes.

Briefly, the code handles the relevant events of a pandemic:

the appearance of the first case,
the infection diffusion by contacts,
the introduction of measures for diffusion limitation such as quarantine,
the activation and implementation of the immunization process.

The distinguishing feature of the model is that individuals are grouped in families. This grouping allows considering two different diffusion speeds: fast among family members and slower when contacts involve two individuals from different families.

Figure 1: relationships between the core classes of the ABSEIR-family model and their variables and methods.

It is perhaps worth describing the evolution of an individual state to sketch the functioning of the model.

An individual’s dynamic is guided by a variable named infectionAge. In the beginning, all the individuals have this variable at zero. The program increases the infectionAge of all the individuals having a non zero value of this variable at each time step.

When an individual has contact with an infectious, s/he can get the infection or not. If infected, the individual enters the latency period, i.e. her/his infectionAge is set to 1 and the variable starts moving ahead with time, but s/he is not infectious. Individuals whose infectionAge is greater than the latency period length (l_l ) become infectious.

At each time step, an infectious meets all her/his family members and m_of randomly chosen non-family members. S/he passes on the infection with probability p_if to family members and p_of to non-family members. The infection can be passed on only if the contacted individual’s infectionAge equals zero and if s/he is not in quarantine.

The infectious phase ends when the infection is discovered (quarantine) or when the individual recovers i.e., the infectionAge is greater than the latency period length plus the infection length parameter (l_i).

At the present stage of development, the code does not handle the virus adverse post-infection evolution. All the infected individuals in this model recover. The infectionAge is set at a negative value at recovery because recovereds stay immune for a while (l_r). Similarly, vaccination set the individual’s infectionAge to a (high) negative value (l_v).

At the present state of the pandemic evolution it is perhaps useful to use the model to get insights into how the family size could affect the vaccination process’s effectiveness. This will be attempted hereafter.

Highlighting the relevance of families size by an ad-hoc example

The relevance of family size in vaccination strategy can be shown using the following ad-hoc example.

Suppose there are two covid-free villages (say village A and B) whose health authorities are about to start vaccinations to avoid the disease spreading.

Villages are identical in the other aspects except for the family size distribution. Each village has 50 inhabitants, but village A has 10 families with five components each, while village B has two five members families and 40 singletons. Five vaccines arrive each day in each village.

Some additional extreme assumptions are made to make differences straightforward.

First, healthy family members are infected for sure by a member who contracted the virus. Second, each individual has the same number of contacts (say n) outside the family and the probability to pass on the virus in external contacts is lower than 1. Symptoms take several days before showing up.

Now, the health authority are about to start the vaccination process and has to decide how to employ the available vaccines.

Intuition would suggest that Village B’s health authority should immunize large families first. Indeed, if case zero arrives at the end of the second vaccination day, the spread of the disease among the population should be limited because the virus can be passed on by external contacts only; and the probability of transmitting the virus in external contacts is lower than in the family.

But, should this strategy be used even by village A health authority?

To answer this question, we compare the family-based vaccination strategy with a random-based vaccination strategy. In a random-based vaccination strategy, we expect one members to be immunized in each family at the end of the second vaccination day. In the family-based vaccination strategy, two families are immunized at the end of the second vaccination day. Now, suppose one of the not-immunized citizens gets the virus at the end of day two. It is easy to verify there will be an infected more in the family-based strategy (all the five components of the family) than in the random-based strategy (4 components because one of them was immunized before). Furthermore, this implies that there will be n additional dangerous external contacts in the family-based strategy than in the random-based strategy.

These observations make us conclude that a random vaccination strategy will slow down the infection dynamics in village A while it will speed up infections in village B, and the opposite is true for the family-based immunization strategy.

Some simulation exercises

In this part of the document, the model described above will be used to compare further the family-based and random-based vaccination strategy to be used against the appearance of a new case (or variant) in a situation similar to that described in the example but with a more realistic setting.

As one can easily imagine, the family size distribution and COVID transmission risk in families are crucial to our simulation exercises. It is therefore important to gather real-world information for these phenomena. Fortunately, recent scientific contributions can help.

Several authors point out that a Poisson distribution is a good statistical model representing the family size distribution. This distribution is suitable because a single parameter characterizes it, i.e., its average, but it has the drawback of having a positive probability for zero value. Recently, Jarosz (2020) confirms the Poisson distribution’s goodness for modeling family size and shows how shifting it by one unit would be a valid alternative to solve the zero family size problem.

Furthermore, average family sizes data can be easily found using, for example, the OECD family database (http://www.oecd.org/social/family/database.htm).

The current version of the database (updated on 06-12-2016) presents data for 2015 with some exceptions. It shows how the average size of families in OECD countries is 2.46, ranging from Mexico (3.93) to Sweden (1.8).

The result in Metlay et al. (2021) guides the choice of the infection in the family parameter. They provide evidence of an overall household infection risk of 10.1%

Simulation exercises consist in parameters sensitivity analysis with respect to the benchmark parameter set reported hereafter.

The simulation initialization is done by loading the family size distribution. Two alternative distributions are used and are tuned to obtain a system with a total number of individuals close to 20000. The two distributions are characterized by different average family sizes (afs) and are shown in figure 2.

Figure 2: two family size distributions used to initialize the simulation. Figures by the dots inform on the frequency of the corresponding size. Black square relates to the distribution with an average of 2.5; red circles relate to the distribution with an average of 3.5

The description of the vaccination strategy gives a possibility to list other relevant parameters. The immunization center is endowed with n_v doses of vaccine at each time starting from time t_v. At time t₀, the state of one of the individuals is changed from susceptible to infected. This subject (case zero) is taken from a family having three susceptibles among their components.

Case zero undergoes the same process as all other following infected individuals described above.

The relevant parameters of the simulations are reported in table 1.

var	description	values	reference
n_i	number of individuals	≅20000
afs	average family size	2.5;3.5	OECD
n_v	number of vaccine doses available at each time	50;100;150
t_v	vaccination starting time	1
t₀	case zero appearance time	10
l_l	length of latency	3	Buran et al 2021
l_i	length of infectious period	5	Buran et al 2021
p_if	probability to infect a family member	0.1	Metlay et al 2021
p_of	probability to infect a non-family individual	0.01;0.02;0.03
m_of	number of non-family contacts of an infectious	10

Table 1: relevant parameters of the model.

We are now going to discuss the results of our simulation exercises. We focus particularly on the number of people infected up to a given point in time.

Due to the presence of random elements, each run has a different trajectory. We limit these effects as much as possible to allow ceteris paribus comparisons. For example, we keep the family size distribution equal across runs by loading the distributions displayed in figure 2 instead of using the run-time random number generator. Again, we set the number of non-family contacts (m_of) equal for all the agents, although the code could set it randomly at each time step. Despite these randomness reductions, significant differences in the dynamics remain within the same parametrization because of randomness in the network of contacts.

To allow comparisons among different parametrizations in the presence of different evolution, we use the cross-section distributions of the total number of infected at the end of the infection process (i.e. time 200).

Figure 3 reports the empirical cumulative distribution function (ecdf) of several parametrizations. To easily read the figure, we put the different charts as in a plane having the average family size (afs) in the abscissa and the number of available vaccines (n_v) in the ordinate. From above, we know two values of afs (i.e. 2.5 and 3.5) and three values of n_v (i.e. 50, 100 and 150) are considered. Therefore figure 3 is made up of 6 charts.

Each chart reports ecdfs corresponding to the three different p_of levels reported in table 1. In particular, circles denote edcfs for p_of = 0.01, squares are for p_of = 0.02 and triangles for p_of = 0.03. At the end, choosing a parameters values triplet (afs, n_v, p_of), two ecdfs are identified. The red one is for the random-based, while the black one is for the family-based vaccination strategy. The family based vaccination strategy prioritizes families with higher number of members not yet infected.

Figure 3 shows mixed results: the random-based vaccination strategy outperforms the family-based one (the red line is above the balck one) for some parameters combinations while the reverse holds for others. In particular, the random-based tends to dominate the family-based strategy in case of larger family (afs = 3.5) and low and high vaccination levels (n_v = 50 and 150). The opposite is true with smaller families at the same vaccination levels. The intermediate level of vaccination provides exceptions.

Figure 3: empirical cumulative distribution function of several parametrizations. The ecdfs is build by taking the number of infected people at period 200 of 100 runs with different random seed for each parametrization.

It is perhaps useful to highlight how, in the model, the family-based vaccination strategy stops the diffusion of a new wave or variant with a significant probability for smaller average family size and low and high vaccination levels (bottom-left and top-left charts) and for large average family size and middle level of vaccination (middle-right chart).

A conclusive note

At present, the model is very simple and can be improved in several directions. The most useful would probably be the inclusion of family-specific information. Setting up the model with additional information on each family member’s age or health state would allow overcoming the “universal mixing assumption” (Watts et al., 2020) currently in the model. Furthermore, additional vaccination strategy prioritization based on multiple criteria (such as vaccinating the families of most fragile or elderly) could be compared.

Initializing the model with census data of a local community could give a chance to analyze a more realistic setting in the wake of Pescarmona et al. (2020) and be more useful and understandable to (local) policy makers (Edmonds, 2020).

Developing the model to provide estimations for hospitalization and mortality is another needed step towards more sound vaccination strategies comparison.

Vaccinating by families could balance direct (vaccinating highest risk individuals) and indirect protection, i.e., limiting the probability the virus reaches most fragiles by vaccinating people with many contacts. It could also have positive economic effects relaunching, for example, family tourism. However, it cannot be implemented at risk of worsening the pandemic.

The present text aims only at posing a question. Further assessments following Squazzoni et al.’s (2020) recommendations are needed.

References

Barton, C.M. et al. (2020) Call for transparency of COVID-19 models. Science, 368(6490), 482-483. doi:10.1126/science.abb8637

Bubar, K.M. et al. (2021) Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science 371, 916–921. doi:10.1126/science.abe6959

Edmonds, B. (2020) What more is needed for truly democratically accountable modelling? Review of Artificial Societies and Social Simulation, 2nd May 2020. https://rofasss.org/2020/05/02/democratically-accountable-modelling/

Jarosz, B. (2021) Poisson Distribution: A Model for Estimating Households by Household Size. Population Research and Policy Review, 40, 149–162. doi:10.1007/s11113-020-09575-x

Metlay J.P., Haas J.S., Soltoff A.E., Armstrong KA. Household Transmission of SARS-CoV-2. (2021) JAMA Netw Open, 4(2):e210304. doi:10.1001/jamanetworkopen.2021.0304

Pescarmona, G., Terna, P., Acquadro, A., Pescarmona, P., Russo, G., and Terna, S. (2020) How Can ABM Models Become Part of the Policy-Making Process in Times of Emergencies – The S.I.S.A.R. Epidemic Model. Review of Artificial Societies and Social Simulation, 20th Oct 2020. https://rofasss.org/2020/10/20/sisar/

Watts, C.J., Gilbert, N., Robertson, D., Droy, L.T., Ladley, D and Chattoe-Brown, E. (2020) The role of population scale in compartmental models of COVID-19 transmission. Review of Artificial Societies and Social Simulation, 14th August 2020. https://rofasss.org/2020/08/14/role-population-scale/

Squazzoni, F., Polhill, J. G., Edmonds, B., Ahrweiler, P., Antosz, P., Scholz, G., Chappin, É., Borit, M., Verhagen, H., Giardini, F. and Gilbert, N. (2020) Computational Models That Matter During a Global Pandemic Outbreak: A Call to Action. Journal of Artificial Societies and Social Simulation, 23(2):10. <http://jasss.soc.surrey.ac.uk/23/2/10.html>. doi: 10.18564/jasss.4298

Giulioni, G. (2020) Should the family size be used in COVID-19 vaccine prioritization strategy to prevent variants diffusion? A first investigation using a basic ABM. Review of Artificial Societies and Social Simulation, 15th April 2021. https://rofasss.org/2021/04/15/famsize/

By Hyesop Shin1 and Yoosoon An2

Introduction

The Agent-based Model: the “North Korean Collective Farm”

Findings

Other Stories

References

Lessons from a session at SocSimFest 2023

By Gary Polhill and Juliette Rouchier

Handling Covid: an evaluation that is still in progress

Modelling for policy making: tension between complexity and elegance?

Cognitive constraints and multiple modellers

Endnotes

Acknowledgements

References

By Fabian Lorig1*, Bart de Bruin2, Melania Borit3, Frank Dignum4, Bruce Edmonds5, Sinéad M. Madden6, Mario Paolucci7, Nicolas Payette8, Loïs Vanhée4

Acknowledgements

References

By Emil Johansson1,2, Vittorio Nespeca3, Mikhail Sirenko4, Mijke van den Hurk5, Jason Thompson6, Kavin Narasimhan7, Michael Belfrage1, 2, Francesca Giardini8, and Alexander Melchior5,9

Motivation

Boy Meets Girl (Too Late)

Modeller’s Adventures in Wonderland

Cinderella – A city’s tale

Conclusions

Acknowledgements

References

By Christian Kammler1, Maarten Jensen1, Rajith Vidanaarachchi2 Cezara Păstrăv1

1 Introduction

2 Rapid Development

3 Model transparency

4 The way forward

Acknowledgements

References

References

By Edmund Chattoe-Brown

References

By Frank Dignum

References

By Mike Bithell and Bruce Edmonds

Model Intercomparison

Model Intercomparison Projects (MIP) in the Climate Community

Other Examples

The Benefits of the Intercomparison Exercises and Collaborative Model Building

Lessons for ABM?

Additional Challenges for ABMs of Social Phenomena

Towards an Initial Proposal

Conclusion

References

By Gianfranco Giulioni

References

For discussion about social simulation research

By Hyesop Shin¹ and Yoosoon An²

By Fabian Lorig^1*, Bart de Bruin², Melania Borit³, Frank Dignum⁴, Bruce Edmonds⁵, Sinéad M. Madden⁶, Mario Paolucci⁷, Nicolas Payette⁸, Loïs Vanhée⁴

By Emil Johansson^1,2, Vittorio Nespeca³, Mikhail Sirenko⁴, Mijke van den Hurk⁵, Jason Thompson⁶, Kavin Narasimhan⁷, Michael Belfrage^{1, 2}, Francesca Giardini⁸, and Alexander Melchior^5,9

By Christian Kammler¹, Maarten Jensen¹, Rajith Vidanaarachchi² Cezara Păstrăv¹