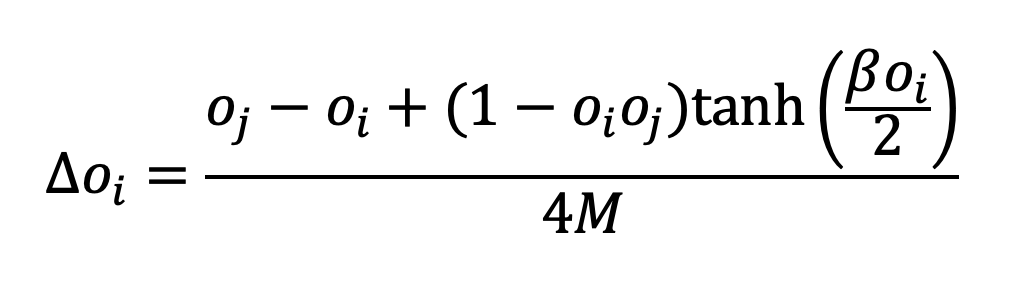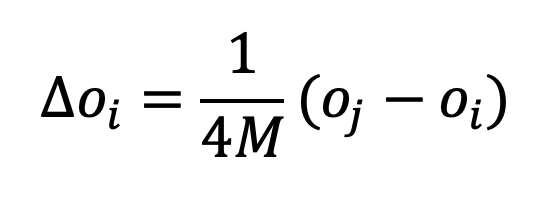Tag Archives: terminology

Content

“One mechanism to rule them all!” A critical comment on an emerging categorization in opinion dynamics

Leave a comment

By Sven Banisch

Department for Sociology, Institute of Technology Futures
Karlsruhe Institute of Technology

It has become common in the opinion dynamics community to categorize different models according to how two agents i and j change their opinions oi and oj in interaction (Flache et al. 2017, Lorenz et al. 2021, Keijzer and Mäs 2022). Three major classes have emerged. First, models of assimilation or positive social influence are characterized by a reduction of opinion differences in interaction as achieved, for instance, by classical models with averaging (French 1956, Friedkin and Johnson 2011). Second, in models with repulsion or negative influence agents may be driven further apart if they are already too distant (Jager and Amblard 2005, Flache and Macy 2011). Third, reinforcement models are characterized by the fact that agents on the same side of the opinion spectrum reinforce their opinion and go more extreme (Martins 2008, Banisch and Olbrich 2019, Baumann et al. 2020). While this categorization is useful for differentiating different classes of models along with their assumptions, for assessing if different model implementations belong to the same class, and for understanding the macroscopic phenomena that can be expected, it is not without problems and may lead to misclassification and misunderstanding.

This comment aims to provide a critical — yet constructive — perspective on this emergent theoretical language for model synthesis and comparison. It directly links to a recent comment in this forum (Carpentras 2023) that describes some of the difficulties that researchers face when developing empirically grounded or validated models of opinion dynamics which often “do not conform to the standard framework of ABM papers”. I have made very similar experiences during a long review process for a paper (Banisch and Shamon 2021) that, to my point of view, rigorously advances argument communication theory — and its models — through experimental research. In large part, the process has been so difficult because authors from different branches of opinion dynamics speak different languages and I feel that some conventions may settle us into a “vicious cycle of isolation” (Carpentras 2020) and closure. But rather than suggesting a divide into theoretically and empirically oriented opinion dynamics research, I would like to work towards a common ground for empirical and theoretical ABM research by a more accurate use of opinion dynamics language.

The classification scheme for basic opinion change mechanisms might be particularly problematic for opinion models that take cognitive mechanisms and more complex opinion structures into account. These often more complex models are required in order to capture linguistic associations observed in real debates, or to better link to a specific experimental design. In this note, I will look at argument communication models (ACMs) (Mäs and Flache 2013, Feliciani et al. 2020, Banisch and Olbrich 2021, Banisch and Shamon 2021) to show how theoretically-inspired model classification can be misleading. I will first show that the classical ACM by Mäs and Flache (2013) has been repeatedly misclassified as a reinforcement model while it is purely averaging when looking at the implied attitude changes. Second, only when biased processing is incorporated into argument-induced opinion changes such that agents favor arguments aligned with their opinion, ACMs become reinforcing or contagious (Lorenz et al. 2021). Third, when biases become large, ACMs may feature patterns of opinion adaptation which — according to the above categorization — are considered as negative influence. 

Opinion change functions for the three model classes

Let us start by looking at the opinion change assumptions entailed in “typical” positive and negative influence and reinforcement models. Following Flache et al. (2017) and Lorenz et al. (2021), we will consider opinion change functions of the following form:

Δoi=f(oi,oj).

That is, the opinion change of agent i is given as a function of i’s opinion and the opinion of an interaction partner j. This is sufficient to characterize an ABM with dyadic interaction where repeatedly two agents with two opinions (oi,oj) are chosen at random and f(oi,oj) is applied. Here we deal with continuous opinions in the interval oi∈[-1,1] in the context of which the model categorizations have been mainly introduced. Notice that some authors refer to f as an influence response function, but as this notion has been introduced in the context of discrete choice models (Lopez-Pintado and Watts 2008, Mäs 2021) governing the behavioral response of agents to the behavior in their neighborhood, we will stick to the term opinion change function (OCF) here. OCFs hence map from two opinions to the induced opinion change: [-1,1]2→R and we can depict them in form of a contour density vector plot as shown in Figure 1.

The most simple form of a positive influence OCF is weighted averaging:

Δoi=μ(oj-oi).

That is, an agent i approaches the opinion of another agent j by a parameter μ times the distance between i and j. This function is shown on the left of Figure 1. If oj<oi  (above the diagonal where oj=oi)  approaches the opinion of  from below. The opinion change is positive indicating a shift to the right (red shades). If oi<oj (below the diagonal) i approaches j from above implying negative opinion change and shift to the left (blue shades). Hence, agents left to the diagonal will shift rightwards, and agents right to the diagonal will shift to the left.

Macroscopically, these models are well-known to converge to consensus on connected networks. However, Deffuant et al. (2000) and Hegselmann and Krause (2002) introduced bounded confidence to circumvent global convergence — and many others have followed with more sophisticated notions of homophily. This class of models (models with similarity bias in Flache et al. 2017) affects the OCF essentially by setting f=0 for opinion pairs that are beyond a certain distance threshold from the diagonal. I will briefly comment on homophily later.

Negative influence can be seen as an extension of bounded confidence such that opinion pairs that are too distant will lead to a repulsive force driving opinions further apart. As the review by Flache et al. (2017), we rely on the OCF from Jager and Amblard (2005) as the paradigmatic case. However, the function shown in Flache et al. (2017) seems to be slightly mistaken so we resort to the original implementation of negative influence by Jager and Amblard (2005):

That is, if the opinion distance |oi–oj| is below a threshold u, we have positive influence as before. If the distance |oi–oj| is larger than a second threshold t, there is repulsive influence such that i is driven away from j. In between these two thresholds, there is a band of no opinion change f(oi,oj)=0 just as for bounded confidence. This function is shown in the middle of Figure 1 (u=0.4 and t=0.7). In this case, we observe a left shift towards a more negative opinion (blue shades) above the diagonal and sufficiently far from it (governed by t). By symmetry, a right shift to a more positive opinion is observed below the diagonal when oi is sufficiently larger than oj. Negative influence is at work in these regions such that an agent i at the right side of the opinion scale (oi<0) will shift towards an even more rightist position when interacting with a leftist agent  with opinion oj>0 (same on the other side).

Notice also that this implementation does not ensure opinions are bound to the interval [-1,1] as negative opinion changes are present even if oi is already at a value of -1. Vice versa for the positive extreme. Typically this is artificially resolved by forcing opinions back to the interval once they exceed it, but a more elegant and psychologically motivated solution has been proposed in Lorenz et al. (2021) by introducing a polarity factor (incorporated below).

Finally, reinforcement models are characterized by the fact that agents on the same side of the opinion scale become stronger in interaction. As pointed out by Lorenz et al. (2021) the most paradigmatic case of reinforcement is simple contagion and the OCF used here for illustration is adopted from their notion:

Δoi=αSign(oj).

That is, agent j signals whether she is in favor (oj>0) or against (oj<0) the object of opinion, and agent i adjusts his opinion by taking a step α in that direction. This means that positive opinion change is observed whenever i meets an agent with an opinion larger than zero. Agent i’s opinion will shift rightwards and become more positive. Likewise, a negative opinion change and shift to the left is observed whenever oj is negative. Notice that, in reinforcement models, opinions assimilate when two agents of opposing opinions interact so that induced opinion changes are similar to positive influence in some regions of the space. As for negative influence, this OCF does not ensure that opinions remain in [-1,1], but see Banisch and Olbrich (2019) for a closely related reinforcement learning model that endogenously remains bound to the interval.

Argument-induced opinion change

Compared to models that fully operate on the level of opinions oi∈[-1,1] and are hence completely specified by an OCF, argument-based models are slightly more complex and the derivation of OCFs from the model rules is not straightforward. But let us first, at least briefly, describe the model as introduced in Banisch and Shamon (2021).

In the model, agents hold a number of M pro- and M counterarguments which may be either zero (disbelief) or one (belief). The opinion of an agent is defined as the number of pro versus con arguments. For instance, if an agent believes 3 pro arguments and only one con argument her opinion will be oi=2. For the purposes of this illustration, we will normalize opinions to lie in between -1 and 1 which is achieved by division through M: oi→oi/M. In interaction, agent j acts as a sender articulating an argument to a receiving agent i. The receiver  takes over that argument with probability

p beta = 1 / (1 + exp(-beta oi dir(arg)))

where the function dir(arg) designates whether the new argument implies positive or negative opinion change. This probability accounts for the fact that agents are more willing to accept information that coheres with their opinion. The free parameter β models the strength of this bias.

From these rules, we can derive an OCF of the form Δoi=f(oi,oj) by considering (i) the probability that  chooses an argument with a certain direction and (ii) the probability that this argument is new to  (see Banisch and Shamon 2021 on the general approach):

Delta 0i=(oj-oi+(1-oioj)tanh(beta*oi/2)))/4M

Notice that this is an approximation because the ACM is not reducible to the level of opinions. First, there are several combinations of pro and con arguments that give rise to the same opinion (e.g. an opinion of +1 is implied by 4 pro and 3 con arguments as well as by 1 pro and 0 con arguments). Second, the probability that ’s argument is new to  depends on the specific argument strings, and there is a tendency that these strings become correlated over time. These correlations lead to memory effects that become visible in the long convergence times of ACMs (Mäs and Flache 2013, Banisch and Olbrich 2021, Banisch and Shamon 2021). The complete mathematical characterization of these effects is far from trivial and beyond the scope of this comment. However, they do not affect the qualitative picture presented here.

  1. Argument models without bias are averaging.

With that OCF it becomes directly visible that it is incorrect to place the original ACM (without bias) within the class of reinforcement models. No bias means β=0, in which case we obtain:

delta oi=(oj-oi)/4M

That is, we obtain the typical positive influence OCF with μ=1/4M shown on the left of Figure 2.

This may appear counter-intuitive (it did in the reviews) because the ACM by Mäs and Flache (2013) generates the idealtypic pattern of bi-polarization in which two opinion camps approach the extreme ends of the opinion scale. But this macro effect is an effect of homophily and the associated changes in the social interaction structure. It is important to note that homophily does not transform an averaging OCF into a reinforcing one. When implemented as bounded confidence it only cuts off certain regions by setting f(oi,oj)=0. Homophily is a social mechanism that acts at another layer and its reinforcing effect in ACMs is conditional on the social configuration of the entire population. In the models, it generates biased argument pools in a way strongly reminiscent of Sunstein’s law of group polarization (2002). That given, the main result by Mäs and Flache (2013) („differentiation without distancing“) is all the more remarkable! But it is at least misleading to associate it with models that implement reinforcement mechanisms (Martins 2008, Banisch and Olbrich 2019, Baumann et al. 2020).

2. Argument models with moderate bias are reinforcing.

It is only when biased processing is enabled that ACMs become what is called reinforcement models. This is clearly visible on the right of Figure 2 where a bias of β=2 has been used. If, in Figure 1, we accounted for the polarity effect, circumventing that opinions exceed the opinion interval   (Lorenz et al. 2021), the match between the right-hand sides of Figures 1 and 2 would be even more remarkable.

This transition from averaging to reinforcement by biased processing shows that the characterization of models in terms of induced opinion changes (OCF) may be very useful and enables model comparison. Namely, at the macro scale, ACMs with moderate bias behave precisely as other reinforcement models. In a dense group, it will lead to what is called group polarization in psychology: the whole group collectively shifts to an extreme opinion at one side of the spectrum. On networks with communities, these radicalization processes may take different directions in different parts of the network and feature collective-level bi-polarization (Banisch and Olbrich 2019).

  1. Argument models with strong bias may appear as negative influence.

Finally, when the β parameter becomes larger, the ACM leaves the regime of reinforcement models and features patterns that we would associate with negative influence. This is shown in the middle of Figure 2. Under strong biased processing, a leftist agent i with an opinion of (say) oi=-0.75 will shift further to the left when encountering a rightist agent j with an opinion of (say) oj=+0.5. Within the existing classes of models, such a pattern is only possible under negative influence. ACMs with biased processing offer a psychologically compelling alternative, and it is an important empirical question whether observed negative influence effects (Bail et al. 2018) are actually due to repulsive forces or due to cognitive biases in information reception.

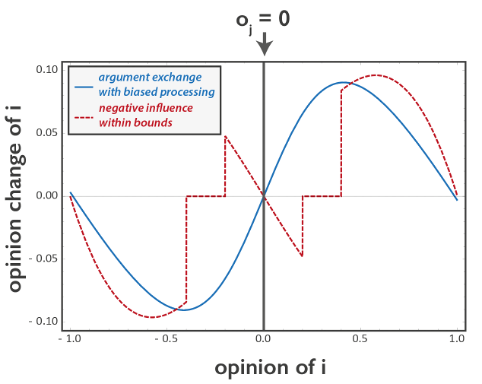
The reader will notice that, when looking at the entire OCF in the space spanned by (oi,oj)∈[-1,1]2, there are qualitative differences between the ACM and the OCF defined in Jager and Amblard (2005). The two mechanisms are different and imply different response functions (OCFs). But for some specific opinion pairs the two functions are hardly discernible as shown in the next figure. The blue solid curve shows the OCF of the argument model for β=5 and an agent i interacting with a neutral agent j, i.e. f(oi,0). The ACM with biased processing is aligned with experimental design and entails a ceiling effect so that maximally positive (negative) agents cannot further increase (decrease) their opinion. To enable fair comparison, we introduce the polarity effect used in Lorenz et al. (2021) to the negative influence OCF ensuring that opinions remain within [-1,1]. That is, for the dashed red curve the factor (1- oi2) (cf. Eq. 6 in Lorenz et al. 2021) is multiplied with the function from Jager and Amblard (2005) using u=0.2 and t=0.4. In this specific case, the shapes of the two OCFs are extremely similar. Experimental test would hardly distinguish the two.

Macroscopically, strong biased processing leads to collective bi-polarization even in the absence of homophily (Banisch and Shamon 2021). This insight has been particularly puzzling and mind-boggling to some of the referees. But the reason for this to happen is precisely the fact that ACMs with biased processing may lead to negative influence opinion change phenomena. This indicates, among other things, that one should be very careful to draw collective-level conclusions such as a depolarizing effect of filter bubbles from empirical signatures of negative influence (Bail et al. 2018). While their argumentation seems at least puzzling on the ground of “classical” negative influence models (Mäs and Bischofberger 2015, Keijzer and Mäs 2022), it could be clearly rejected if the empirical negative influence effects are attributed to the cognitive mechanism of biased processing. In ACMs, homophily generally enhances polarization tendencies (Banisch and Shamon 2021).

What to take from here?

Opinion dynamics is at a challenging stage! We have problems with empirical validation (Sobkowicz 2009, Flache et al. 2017) but seem to not sufficiently acknowledge those who advance the field into that direction (Chattoe-Brown 2022, Keijzer 2022, Carpentras 2023). It is greatly thanks to the RofASSS forum that these deficits have become visible. Against that background, this comment is written as a critical one, because developing models with a tight connection to empirical data does not always fit with the core model classes derived from research with a theoretical focus.

The prolonged review process for Banisch and Shamon (2021) — strongly reminiscent of the patterns described by Carpentras (2023) — revealed that there is a certain preference in the community to draw on models building on “opinions” as the smallest and atomic analytical unit. This is very problematic for opinion models that take cognitive mechanisms and complexity into due account. Moreover, we barely see “opinions” in empirical measurements, but rather observe argumentative statements and associations articulated on the web and elsewhere. To my point of view, we have to acknowledge that opinion dynamics is a field that cannot isolate itself from psychology and cognitive science because intra-individual mechanisms of opinion change are at the core of all our models. And just as new phenomena may emerge as we go from individuals to groups or populations, surprises may happen when a cognitive layer of beliefs, arguments, and their associations is underneath. We can treat these emergent effects as mere artifacts of expendable cognitive detail, or we can truly embrace the richness of opinion dynamics as a field spanning multiple levels from cognition to macro social phenomena.

On the other hand, the analysis of the OCF “emerging” from argument exchange also points back to the atomic layer of opinions as a useful reference for model comparisons and synthesis. Specific patterns of opinion updates emerge in any opinion dynamics model however complicated its rules and their implementation might be. For understanding macro effects, more complicated psychological mechanisms may be truly relevant only in so far as they imply qualitatively different OCFs. The functional form of OCFs may serve as an anchor of reference for “model translations” allowing us to better understand the role of cognitive complexity in opinion dynamics models.

What this research comment — clearly overstating at the very front — also aims to show is that modeling based in psychology and cognitive science does not automatically mean we leave behind the principles of parsimony. The ACM with biased processing has only a single effective parameter (β) but is rich enough to span over three very different classes of models. It is averaging if β=0,  it behaves like a reinforcement model with moderate bias (β=2), and may look like negative influence for larger values of . For me, this provides part of an explanation for the misunderstandings that we experienced in the review process for Banisch and Shamon (2021). It’s just inappropriate to talk about ACMs with biased processing within the categories of “classical” models of assimilation, repulsion, and reinforcement. So the review process has been insightful, and I am very grateful that traditional Journals afford such productive spaces of scientific discourse. My main “take-home” from this whole enterprise is that current language enjoins caution to not mix opinion change phenomena with opinion change mechanisms.

Acknowledgements

I am grateful to the Sociology and Computational Social Science group at KIT  — Michael Mäs, Fabio Sartori, and Andreas Reitenbach — for their feedback on a preliminary version of this commentary. I also thank Dino Carpentras for his preliminary reading.

This comment would not have been written without the three anonymous referees at Sociological Methods and Research.

References

Flache, A., Mäs, M., Feliciani, T., Chattoe-Brown, E., Deffuant, G., Huet, S., & Lorenz, J. (2017). Models of social influence: Towards the next frontiers. Journal of Artificial Societies and Social Simulation, 20(4),2 http://jasss.soc.surrey.ac.uk/20/4/2.html. DOI:10.18564/jasss.3521

Lorenz, J., Neumann, M., & Schröder, T. (2021). Individual attitude change and societal dynamics: Computational experiments with psychological theories. Psychological Review, 128(4), 623. https://psycnet.apa.org/doi/10.1037/rev0000291

Keijzer, M. A., & Mäs, M. (2022). The complex link between filter bubbles and opinion polarization. Data Science, 5(2), 139-166. DOI:10.3233/DS-220054

French Jr, J. R. (1956). A formal theory of social power. Psychological review, 63(3), 181. DOI:10.1037/h0046123

Friedkin, N. E., & Johnsen, E. C. (2011). Social influence network theory: A sociological examination of small group dynamics (Vol. 33). Cambridge University Press.

Jager, W., & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-based simulation model of attitude change. Computational & Mathematical Organization Theory, 10, 295-303. https://link.springer.com/article/10.1007/s10588-005-6282-2

Flache, A., & Macy, M. W. (2011). Small Worlds and Cultural Polarization. Journal of Mathematical Sociology, 35, 146-176. https://doi.org/10.1080/0022250X.2010.532261

Martins, A. C. (2008). Continuous opinions and discrete actions in opinion dynamics problems. International Journal of Modern Physics C, 19(04), 617-624. https://doi.org/10.1142/S0129183108012339

Banisch, S., & Olbrich, E. (2019). Opinion polarization by learning from social feedback. The Journal of Mathematical Sociology, 43(2), 76-103. https://doi.org/10.1080/0022250X.2018.1517761

Baumann, F., Lorenz-Spreen, P., Sokolov, I. M., & Starnini, M. (2020). Modeling echo chambers and polarization dynamics in social networks. Physical Review Letters, 124(4), 048301. https://doi.org/10.1103/PhysRevLett.124.048301

Carpentras, D. (2023). Why we are failing at connecting opinion dynamics to the empirical world. 8th March 2023. https://rofasss.org/2023/03/08/od-emprics/

Banisch, S., & Shamon, H. (2021). Biased Processing and Opinion Polarisation: Experimental Refinement of Argument Communication Theory in the Context of the Energy Debate. Available at SSRN 3895117. The most recent version is available as an arXiv preprint arXiv:2212.10117.

Carpentras, D. (2020) Challenges and opportunities in expanding ABM to other fields: the example of psychology. Review of Artificial Societies and Social Simulation, 20th December 2021. https://rofasss.org/2021/12/20/challenges/

Mäs, M., & Flache, A. (2013). Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PloS One, 8(11), e74516. https://doi.org/10.1371/journal.pone.0074516

Feliciani, T., Flache, A., & Mäs, M. (2021). Persuasion without polarization? Modelling persuasive argument communication in teams with strong faultlines. Computational and Mathematical Organization Theory, 27, 61-92. https://link.springer.com/article/10.1007/s10588-020-09315-8

Banisch, S., & Olbrich, E. (2021). An Argument Communication Model of Polarization and Ideological Alignment. Journal of Artificial Societies and Social Simulation, 24(1). https://www.jasss.org/24/1/1.html
DOI: 10.18564/jasss.4434

Lorenz, J., Neumann, M., & Schröder, T. (2021). Individual attitude change and societal dynamics: Computational experiments with psychological theories. Psychological Review, 128(4), 623. https://psycnet.apa.org/doi/10.1037/rev0000291

Mäs, M. (2021). Interactions. In Research Handbook on Analytical Sociology (pp. 204-219). Edward Elgar Publishing.

Lopez-Pintado, D., & Watts, D. J. (2008). Social influence, binary decisions and collective dynamics. Rationality and Society, 20(4), 399-443. https://doi.org/10.1177/1043463108096787

Deffuant, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(01n04), 87-98.

Hegselmann, R., & Krause, U. (2002). Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation. Journal of Artificial Societies and Social Simulation, 5(3),2. https://jasss.soc.surrey.ac.uk/5/3/2.html

Sunstein, C. R. (2002). The Law of Group Polarization. The Journal of Political Philosophy, 10(2), 175-195. https://dx.doi.org/10.2139/ssrn.199668

Bail, C. A., Argyle, L. P., Brown, T. W., Bumpus, J. P., Chen, H., Hunzaker, M. F., … & Volfovsky, A. (2018). Exposure to opposing views on social media can increase political polarization. Proceedings of the National Academy of Sciences, 115(37), 9216-9221. https://doi.org/10.1073/pnas.1804840115

Mäs, M., & Bischofberger, L. (2015). Will the personalization of online social networks foster opinion polarization? Available at SSRN 2553436. https://dx.doi.org/10.2139/ssrn.2553436

Sobkowicz, P. (2009). Modelling opinion formation with physics tools: Call for closer link with reality. Journal of Artificial Societies and Social Simulation, 12(1), 11. https://www.jasss.org/12/1/11.html

Chattoe-Brown, E. (2022). If You Want To Be Cited, Don’t Validate Your Agent-Based Model: A Tentative Hypothesis Badly In Need of Refutation. Review of Artificial Societies and Social Simulation, 1 Feb 2022. https://rofasss.org/2022/02/01/citing-od-models/

Keijzer, M. (2022). If you want to be cited, calibrate your agent-based model: a reply to Chattoe-Brown. Review of Artificial Societies and Social Simulation.  9th Mar 2022. https://rofasss.org/2022/03/09/Keijzer-reply-to-Chattoe-Brown

Banisch, S. (2023) “One mechanism to rule them all!” A critical comment on an emerging categorization in opinion dynamics. Review of Artificial Societies and Social Simulation, 26 Apr 2023. https://rofasss.org/2023/04/26/onemechanism

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Content

Models in Social Psychology and Agent-Based Social simulation – an interdisciplinary conversation on similarities and differences

Leave a comment

By Nanda Wijermans, Geeske Scholz, Rocco Paolillo, Tobias Schröder, Emile Chappin, Tony Craig, and Anne Templeton

Introduction

Understanding how individual or group behaviour are influenced by the presence of others is something both social psychology and agent-based social simulation are concerned with. However, there is only limited overlap between these two research communities, which becomes clear when terms such as “variable”, “prediction”, or “model” come into play, and we build on their different meanings. This situation challenges us when working together, since it complicates the uptake of relevant work from each community and thus hampers the potential impact that we could have when joining forces.

We[1] – a group of social psychologists and social simulation modellers – sought to clarify the meaning of models and modelling from an interdisciplinary perspective involving these two communities. This occurred while starting our collaboration to formalise ‘social identity approaches’ (SIA). It was part of our journey to learn how to communicate and understand each other’s work, insights, and arguments during our discussions.

We present a summary of our reflections on what we learned from and with each other in this paper, which we intend to be part of a conversation, complementary to existing readings on ABM and social psychology (e.g., Lorenz, Neumann, & Schröder, 2021; Smaldino, 2020; Smith & Conrey, 2007). Complementary, because one comes to understand things differently when engaging directly in conversation with people from other communities, and we hope to extend this from our network to the wider social simulation community.

What are variable- and agent-based models?

We started the discussion by describing to each other what we mean when we talk about “a model” and distinguishing between models in the two communities as variable-based models in social psychology and agent-based modelling in social simulation.

Models in social psychology generally come in two interrelated variants. Theoretical models, usually stated verbally and typically visualised with box-and-arrow diagrams as in Figure 1 (left), reflect assumptions of causal (but also correlational) relations between a limited number of variables. Statistical models are often based in theory and fitted to empirical data to test how well the explanatory variables predict the dependent variables, following the causal assumptions of the corresponding theoretical model. We therefore refer to social-psychological models as variable-based models (VBM). Core concepts are prediction and effect size. A prediction formulates whether one variable or combination of more variables causes an effect on an outcome variable. The effect size is the result of testing a prediction by indicating the strength of that effect, usually in statistical terms, the magnitude of variance explained by a statistical model.

It is good to realise that many social psychologists strive for a methodological gold standard using controlled behavioural experiments. Ideally, one predicts data patterns based on a theoretical model, which is then tested with data. However, observations of the real world are often messier. Inductive post hoc explanations emerge when empirical findings are unexpected or inconclusive. The discovery that much experimental work is not replicable has led to substantial efforts to increase the rigour of the methods, e.g., through the preregistration of experiments (Eberlen, Scholz & Gagliolo, 2017).

Models in Social Simulation come in different forms – agent-based models, mathematical models, microsimulations, system dynamic models etc – however here we focus on agent-based modelling as it is the dominant modelling approach within our SIAM network. Agent-based models reflect heterogeneous and autonomous entities (agents) that interact with each other and their environments over time (Conte & Paolucci, 2014; Gilbert & Troitzsch, 2005). Relationships between variables in ABMs need to be stated formally (equations or logical statements) in order to implement theoretical/empirical assumptions in a way that is understandable by a computer. An agent-based model can reflect assumptions about causal relations between as many variables as the modeller (team) intends to represent. Agent-based models are often used to help understand[2] why and how observed (macro) patterns arise by investigating the (micro/meso) processes underlying them (see Fig 1, right).

The extent to which social simulation models relate to data ranges from ‘no data used whatsoever’ to ‘fitting every variable value’ to empirical data. Put differently, the way one uses data does not define the approach. Note that assumptions based on theory and/or empirical observations do not suffice but require additional assumptions to make the model run.

Fig. 1: Visualisation of what a variable-based model in social psychology is (left) and what an agent-based model in social simulation is (right).

Comparing models

The discussion then moved from describing the meaning of “a model” to comparing similarities and differences between the concepts and approaches, but also what seems similar but is not…

Similar. The core commonalities of models in social psychology (VBM) and agent-based social simulation (ABM) are 1) the use of models to specify, test and/or explore (causal) relations between variables and 2) the ability to perform systematic experiments, surveys, or observations for testing the model against the real world. This means that words like ‘experimental design’, ‘dependent, independent and control variables’ have the same meaning. At the same time some aspects that are similar are labelled differently. For instance, the effect size in VBMs reflects the magnitude of the effect one can observe. In ABMs the analogy would be the sensitivity analysis, where one tests for the importance or role of certain variables on the emerging patterns in the simulation outcomes.

False Friends. There are several concepts that are given similar labels, but have different meanings. These are particularly important to be aware of in interdisciplinary settings as they can present “false friends”. The false friends we unpacked in our conversations are the following:

  • Model: whether the model is variable-based in social psychology (VBM) or agent-based in social simulation (ABM). The VBM focuses on the relation between two or a few variables typically in one snapshot of time, whereas the ABM focuses on the causal relations (mechanisms/processes) between (entities (agents) containing a number of) variables and simulates the resulting interactions over time.
  • Prediction: in VBMs a prediction is a variable-level claim, stating the expected magnitude of a  relation between two or few variables. In ABMs prediction would instead be a claim about the future real-world system-level developments on the basis of observed phenomena in the simulation outcomes. In case such prediction is not the model purpose (which is likely), each future simulated system state is sometimes labelled nevertheless as a prediction, though it doesn’t mean to be necessarily accurate as a prediction to the real-world future. Instead, it can for example be a full explanation of the mechanisms required to replicate the particular phenomenon or a possible trajectory of which reality is just one. 
  • Variable: here both types of models have variables (a label of some ‘thing’ that can have a certain ‘value’). In ABMs there can be many variables, some that have the same function as the variables in VBM (i.e., denoting a core concept and its value). Additionally, ABMs also have (many) variables to make things work.
  • Effect size: in VBM the magnitude of how much the independent variable can explain a dependent variable. In ABM the analogy would be sensitivity analysis, to determine the extent to which simulation outcomes are sensitive to changes in input settings. Note that, while effect size is critical in VBMs, in ABMs small effect sizes in micro interactions can lead toward large effects on the macro level.
  • Testing: VBMs usually test models using some form of hypothesis testing, whereas ABMs can be tested in very different ways (see David et al (2019)), depending on the purpose they have (e.g., explanation, theoretical exposition, prediction, see Edmonds et al. (2019)), and on different levels. For instance, testing can relate to the verification of the implementation of the model (software development specific), to make sure the model behaves as designed. However, testing can also relate to validation – checking whether the model lives up to its purpose – for instance testing the results produced by the ABM against real data if the aim is prediction of the real world-state.
  • Internal validity: in VBM this is to assure the causal relation between variables and their effect size. In ABMs it refers to the plausibility in assumptions and causal relations used in the model (design), e.g., by basing these on expert knowledge, empirical insights, or theory rather than on the modeller’s intuition only.

Differences. There are several differences when it comes to VBM and ABM. Firstly, there is a difference in what a model should replicate, i.e., the target of the model: in social psychology the focus tends to be on the relations between variables underlying behaviour, whereas in ABM it is usually on the macro-level patterns/structures that emerge. Also, the concept of causality differs in psychology, VBM models are predominantly built under the assumption of linear causality[3], with statistical models aiming to quantify the change in the dependent variable due to (associated) change in the independent variable. A causality or correlation often derived with “snapshot data”, i.e., one moment in time and one level of analysis. In ABMs, on the other hand, causality appears as a chain of causal relations that occur over time. Moreover, it can be non-linear (including multicausality, nonlinearity, feedback loops and/or amplifications of models’ outcomes). Lastly, the underlying philosophy can differ tremendously concerning the number of variables that are taken into consideration. By design, in social psychology one seeks to isolate the effects of variables, maintaining a high level of control to be confident about the effect of independent variables or the associations between variables. For example, by introducing control variables in regression models or assuring random allocation of participants in isolated experimental conditions. Whereas in ABMs, there are different approaches/preferences: KISS versus KIDS (Edmonds & Moss, 2004). KISS (Keep It Simple Stupid) advocates for keeping it simple as possible: only complexify if the simple model is not adequate. KIDS (Keep It Descriptive Stupid), on the other end of the spectrum, embraces complexity by relating to the target phenomenon as much as one can and only simplify when evidence justifies it. Either way, the idea of control in ABM is to avoid an explosion of complexity that impedes the understanding of the model, that can lead to e.g., causes misleading interpretations of emergent outcomes due to meaningless artefacts.

We summarise some core take-aways from our comparison discussions in Table 1.

Table 1. Comparing models in social psychology and agent-based social simulation

Social psychology (VBM)Social Simulation (ABM)
AimTheory development and prediction (variable level)Not predefined. Can vary widely purpose. (system level)
Model targetReplicate and test relations between variablesReproduce and/or explain a social phenomenon – the macro level pattern
Composed ofVariables and relations between themAgents, environment & interactions
Strive forHigh control, (low number of variables and relations ReplicationPurpose-dependent. Model complexity: represent what is needed, not more, not less.
TestingHypotheses testing using statistics, including possible measuring the effect size a relation to assess confidence in the variable’s importance’Purpose-dependent. Can refer to verification, validation, sensitivity analysis or all of them. See text and refs under false friends.
Causality(or correlation) between variables Linear representationBetween variables and/or model entities.
Non-linear representation
Theory developmentCritical reflection on theory through confirmation. Through hypothesis testing (a prediction) theory gets validated or (if not confirmed) input for reconsideration of the theory.IFF aim of model, ways of doing is not predefined. It can be reproducing the theory prediction with or without internal validity. ABMs can further help to identify gaps in existing theory.
DynamismLittle – often within snapshot causalityCore – within snapshot and over time causality
External validity(the ability to say something about the actual target/ empirical  phenomenon)VBM aims at generalisation and has predictive value for the phenomenon in focus. VBMs in lab experiments are often criticised for their weak external validity, considered high for field experiments.ABMs insights are about the model, not directly about the real world. Without making predictive claims, they often do aim to say something about the real world.

Beyond blind spots, towards complementary powers

We shared the result of our discussions, the (seemingly) communalities and differences between models in social psychology and agent-based social simulation. We allowed for a peek into the content of our interdisciplinary journey as we invested time, allowed for trust to grow, and engaged in open communication. All of this was needed in the attempt to uncover conflicting ways of seeing and studying the social identity approach (SIA). This investment was crucial to be able to make progress in formalising SIA in ways that enable for deeper insights – formalisations that are in line with SIA theories, but also to push the frontiers in SIA theory. Joining forces allows for deeper insights, as VBM and ABM complement and challenge each other, thereby advancing the frontiers in ways that cannot be achieved individually (Eberlen, Scholz & Gagliolo, 2017; Wijermans et al. 2022,). SIA social psychologists bring to the table the deep understanding of the many facets of SIA theories and can engage in the negotiation dance of the formalisation process adding crucial understanding of the theories, placed in their theoretical context. Social psychology in general can point to empirically supported causal relations between variables, and thereby increase the realism of the assumptions of agents (Jager, 2017; Templeton & Neville 2020). Agent-based social simulation, on the other hand, pushes for over-time causality representation, bringing to light (logical) gaps of a theory and providing explicitness and thereby adding to the development of testable (extended) forms of (parts of) a theory, including the execution of those experiments that are hard or impossible in controlled experiments. We thus started our journey, hoping to shed some light on blind spots and releasing our complementary powers in the formalisation of SIA.

To conclude, we felt that having a conversation together led to a qualitatively different understanding than would have been the case had we all ‘just’ reading informative papers. These conversations reflect a collaborative research process (Schlüter et al. 2019). In this RofASSS paper, we strive for widening this conversation to the social simulation community, connecting with others about our thoughts as well as hearing your experiences, thoughts and learnings while being on an interdisciplinary journey with minds shaped by variable-based or agent-based models, or both.

Acknowledgements

The many conversations we had in this stimulating scientific network since 2020 were funded by the the  Deutsche Forschungsgemeinschaft (DFG- 432516175)

References

Conte, R., & Paolucci, M. (2014). On agent-based modeling and computational social science. Frontiers in psychology, 5, 668. DOI:10.3389/fpsyg.2014.00668

David, N., Fachada, N., & Rosa, A. C. (2017). Verifying and validating simulations. In Simulating social complexity (pp. 173-204). Springer, Cham. DOI:10.1007/978-3-319-66948-9_9

Eberlen, J., Scholz, G., & Gagliolo, M. (2017). Simulate this! An introduction to agent-based models and their power to improve your research practice. International Review of Social Psychology, 30(1). DOI:10.5334/irsp.115/

Edmonds, B., & Moss, S. (2004). From KISS to KIDS–an ‘anti-simplistic’modelling approach. In International workshop on multi-agent systems and agent-based simulation (pp. 130-144). Springer, Berlin, Heidelberg. DOI:10.1007/978-3-540-32243-6_11

Edmonds, B., Le Page, C., Bithell, M., Chattoe-Brown, E., Grimm, V., Meyer, R., Montañola-Sales, C., Ormerod, P., Root, H. and Squazzoni, F. (2019) ‘Different Modelling Purposes’ Journal of Artificial Societies and Social Simulation 22 (3) 6 <http://jasss.soc.surrey.ac.uk/22/3/6.html>. doi: 10.18564/jasss.3993

Gilbert, N., & Troitzsch, K. (2005). Simulation for the social scientist. McGraw-Hill Education (UK).

Jager, W. (2017). Enhancing the realism of simulation (EROS): On implementing and developing psychological theory in social simulation. Journal of Artificial Societies and Social Simulation, 20(3). https://jasss.soc.surrey.ac.uk/20/3/14.html

Lorenz, J., Neumann, M., & Schröder, T. (2021). Individual attitude change and societal dynamics: Computational experiments with psychological theories. Psychological Review, 128(4), 623-642.  https://doi.org/10.1037/rev0000291

Smaldino, P. E. (2020). How to Translate a Verbal Theory Into a Formal Model. Social Psychology, 51(4), 207–218. http://doi.org/10.1027/1864-9335/a000425

Schlüter, M., Orach, K., Lindkvist, E., Martin, R., Wijermans, N., Bodin, Ö., & Boonstra, W. J. (2019). Toward a methodology for explaining and theorizing about social-ecological phenomena. Current Opinion in Environmental Sustainability, 39, 44-53. DOI:10.1016/j.cosust.2019.06.011

Smith, E.R. & Conrey, F.R. (2007): Agent-based modeling: a new approach for theory building in social psychology. Pers Soc Psychol Rev, 11:87-104. DOI:10.1177/1088868306294789

Templeton, A., & Neville, F. (2020). Modeling collective behaviour: insights and applications from crowd psychology. In Crowd Dynamics, Volume 2 (pp. 55-81). Birkhäuser, Cham. DOI:10.1007/978-3-030-50450-2_4

Wijermans, N., Schill, C., Lindahl, T., & Schlüter, M. (2022). Combining approaches: Looking behind the scenes of integrating multiple types of evidence from controlled behavioural experiments through agent-based modelling. International Journal of Social Research Methodology, 1-13. DOI:10.1080/13645579.2022.2050120

Notes 

[1] Most VBMs are linear (or multilevel linear models), but not all.  In the case of non-normally distributed data changes the tests that are used.

[2] We are researchers keen to use, extend, and test the social identity approach (SIA) using agent-based modelling. We started from interdisciplinary DFG network project (SIAM: Social Identity in Agent-based Models, https://www.siam-network.online/) and now form a continuous special-interest group at the European Social Simulation Association (ESSA) http://www.essa.eu.org/.

[3] ABMs can cater to diverse purposes, e.g., description, explanation, prediction, theoretical exploration, illustration, etc. (Edmonds et al., 2019).

Wijermans, N., Scholz, G., Paolillo, R., Schröder, T., Chappin, E., Craig, T. and Templeton, A. (2022) Models in Social Psychology and Agent-Based Social simulation - an interdisciplinary conversation on similarities and differences. Review of Artificial Societies and Social Simulation, 4 Oct 2022. https://rofasss.org/2022/10/04/models-in-spabss/

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)

Content

Today We Have Naming Of Parts: A Possible Way Out Of Some Terminological Problems With ABM

2 Comments

By Edmund Chattoe-Brown


Today we have naming of parts. Yesterday,
We had daily cleaning. And tomorrow morning,
We shall have what to do after firing. But to-day,
Today we have naming of parts. Japonica
Glistens like coral in all of the neighbouring gardens,
And today we have naming of parts.
(Naming of Parts, Henry Reed, 1942)

It is not difficult to establish by casual reading that there are almost as many ways of using crucial terms like calibration and validation in ABM as there are actual instances of their use. This creates several damaging problems for scientific progress in the field. Firstly, when two different researchers both say they “validated” their ABMs they may mean different specific scientific activities. This makes it hard for readers to evaluate research generally, particularly if researchers assume that it is obvious what their terms mean (rather than explaining explicitly what they did in their analysis). Secondly, based on this, each researcher may feel that the other has not really validated their ABM but has instead done something to which a different name should more properly be given. This compounds the possible confusion in debate. Thirdly, there is a danger that researchers may rhetorically favour (perhaps unconsciously) uses that, for example, make their research sound more robustly empirical than it actually is. For example, validation is sometimes used to mean consistency with stylised facts (rather than, say, correspondence with a specific time series according to some formal measure). But we often have no way of telling what the status of the presented stylised facts is. Are they an effective summary of what is known in a field? Are they the facts on which most researchers agree or for which the available data presents the clearest picture? (Less reputably, can readers be confident that they were not selected for presentation because of their correspondence?) Fourthly, because these terms are used differently by different researchers it is possible that valuable scientific activities that “should” have agreed labels will “slip down the terminological cracks” (either for the individual or for the ABM community generally). Apart from clear labels avoiding confusion for others, they may help to avoid confusion for you too!

But apart from these problems (and there may be others but these are not the main thrust of my argument here) there is also a potential impasse. There simply doesn’t seem to be any value in arguing about what the “correct” meaning of validation (for example) should be. Because these are merely labels there is no objective way to resolve this issue. Further, even if we undertook to agree the terminology collectively, each individual would tend to argue for their own interpretation without solid grounds (because there are none to be had) and any collective decision would probably therefore be unenforceable. If we decide to invent arbitrary new terminology from scratch we not only run the risk of adding to the existing confusion of terms (rather than reducing it) but it is also quite likely that everyone will find the new terms unhelpful.

Unfortunately, however, we probably cannot do without labels for these scientific activities involved in quality controlling ABMs. If we had to describe everything we did without any technical shorthand, presenting research might well become impossibly unwieldy.

My proposed solution is therefore to invent terms from scratch (so we don’t end up arguing about our different customary usages to no purpose) but to do so on the basis of actual scientific practices reported in published research. For example, we might call the comparison of corresponding real and simulated data (which at least has the endorsement of the much used Gilbert and Troitzsch 2005 – see pp. 15-19 – to be referred to as validation) CORAS – Comparison Of Real And Simulated. Similarly, assigning values to parameters given the assumptions of model “structures” might be called PANV – Parameters Assigned Numerical Values.

It is very important to be clear what the intention is here. Naming cannot solve scientific problems or disagreements. (Indeed, failure to grasp this may well be why our terminology is currently so muddled as people try to get their different positions through “on the nod”.) For example, if we do not believe that correspondence with stylised facts and comparison measures on time series have equivalent scientific status then we will have to agree distinct labels for them and have the debate about their respective value separately. Perhaps the former could be called COSF – Comparison Of Stylised Facts. But it seems plainly easier to describe specific scientific activities accurately and then find labels for them than to have to wade through the existing marsh of ambiguous terminology and try to extract the associated science. An example of a practice which does not seem to have even one generally agreed label (and therefore seems to be neglected in ABM as a practice) is JAMS – Justifying A Model Structure. (Why are your agents adaptive rather than habitual or rational? Why do they mix randomly rather than in social networks?)

Obviously, there still needs to be community agreement for such a convention to be useful (and this may need to be backed institutionally for example by reviewing requirements). But the logic of the approach avoids several existing problems. Firstly, while the labels are useful shorthand, they are not arbitrary. Each can be traced back to a clearly definable scientific practice. Secondly, this approach steers a course between the Scylla of fruitless arguments from current muddled usage and the Charybdis of a novel set of terminology that is equally unhelpful to everybody. (Even if people cannot agree on labels, they knew how they built and evaluated their ABMs so they can choose – or create – new labels accordingly.) Thirdly, the proposed logic is extendable. As we clarify our thinking, we can use it to label (or improve the labels of) any current set of scientific practices. We will do not have to worry that we will run out of plausible words in everyday usage.

Below I suggest some more scientific practices and possible terms for them. (You will see that I have also tried to make the terms as pronounceable and distinct as possible.)

Practice Term
Checking the results of an ABM by building another.[1] CAMWA (Checking A Model With Another).
Checking ABM code behaves as intended (for example by debugging procedures, destructive testing using extreme values and so on). TAMAD (Testing A Model Against Description).
Justifying the structure of the environment in which agents act. JEM (Justifying the Environment of a Model): This is again a process that may pass unnoticed in ABM typically. For example, by assuming that agents only consider ethnic composition, the Schelling Model (Schelling 1969, 1971) does not “allow” locations to be desirable because, for example, they are near good schools. This contradicts what was known empirically well before (see, for example, Rossi 1955) and it isn’t clear whether simply saying that your interest is in an “abstract” model can justify this level of empirical neglect.
Finding out what effect parameter values have on ABM behaviour. EVOPE (Exploring Value Of Parameter Effects).
Exploring the sensitivity of an ABM to structural assumptions not justified empirically (see Chattoe-Brown 2021). ESOSA (Exploring the Sensitivity Of Structural Assumptions).

Clearly this list is incomplete but I think it would be more effective if characterising the scientific practices in existing ABM and naming them distinctively was a collective enterprise.

Acknowledgements

This research is funded by the project “Towards Realistic Computational Models Of Social Influence Dynamics” (ES/S015159/1) funded by ESRC via ORA Round 5 (PI: Professor Bruce Edmonds, Centre for Policy Modelling, Manchester Metropolitan University: https://gtr.ukri.org/projects?ref=ES%2FS015159%2F1).

Notes

[1] It is likely that we will have to invent terms for subcategories of practices which differ in their aims or warranted conclusions. For example, rerunning the code of the original author (CAMWOC – Checking A Model With Original Code), building a new ABM from a formal description like ODD (CAMUS – Checking A Model Using Specification) and building a new ABM from the published description (CAMAP – Checking A Model As Published, see Chattoe-Brown et al. 2021).

References

Chattoe-Brown, Edmund (2021) ‘Why Questions Like “Do Networks Matter?” Matter to Methodology: How Agent-Based Modelling Makes It Possible to Answer Them’, International Journal of Social Research Methodology, 24(4), pp. 429-442. doi:10.1080/13645579.2020.1801602

Chattoe-Brown, Edmund, Gilbert, Nigel, Robertson, Duncan A. and Watts Christopher (2021) ‘Reproduction as a Means of Evaluating Policy Models: A Case Study of a COVID-19 Simulation’, medRXiv, 23 February. doi:10.1101/2021.01.29.21250743

Gilbert, Nigel and Troitzsch, Klaus G. (2005) Simulation for the Social Scientist, second edition (Maidenhead: Open University Press).

Rossi, Peter H. (1955) Why Families Move: A Study in the Social Psychology of Urban Residential Mobility (Glencoe, IL, Free Press).

Schelling, Thomas C. (1969) ‘Models of Segregation’, American Economic Review, 59(2), May, pp. 488-493. (available at https://www.jstor.org/stable/1823701)

Chattoe-Brown, E. (2022) Today We Have Naming Of Parts: A Possible Way Out Of Some Terminological Problems With ABM. Review of Artificial Societies and Social Simulation, 11th January 2022. https://rofasss.org/2022/01/11/naming-of-parts/

© The authors under the Creative Commons’ Attribution-NoDerivs (CC BY-ND) Licence (v4.0)